Spaß mit Rotationen und Transformationen in Processing.py

Rotationen und Transformationen sind sehr nützliche Operationen in der Computergraphik. Doch manches Mal ist es nicht so ganz einsichtig, für was man sie braucht und wie man sie einsetzt. Daher habe ich ein nettes Beispiel aus dem Buch »Math Adventures with Python« von Peter Farrell ausgegraben und aufgebohrt, das aufzeigen soll, wie man rotate() und translate() in Processing.py – dem Python-Mode von Processing – nutzt:

Ausgangspunkt war die Idee, zwölf kleine Quadrate im Kreis regelmäßig anzuordnen und sie um diesen Kreis rotieren zu lassen. Das ist in Processing.py schnell erledigt:

t = 0

def setup():
    size(600, 600)
    this.surface.setTitle("Rotationen")
    rectMode(CENTER)

def draw():
    global t
    colorMode(RGB)
    background("#2b3e50")
    translate(width/2, height/2)
    rotate(radians(t))
    for _ in range(12):
        rect(200, 0, 50, 50)
        rotate(radians(360, 12))
    t += 1

Wenn Ihr diesen Sketch laufen laßt, sehr Ihr zwölf Quadrate, die sich majestätisch im Kreis drehen. Doch was ist, wenn jedes dieser Quadrate auch noch um die eigene Achse rotieren soll. Ein Hindernis habe ich schon im setup() beseitigt: Da per Default der Rotationspunkt eines Rechtecks die obere linke Ecke dieses Rechtecks ist, habe ich mit rectMode(CENTER) diesen Rotationspunkt in die Mitte des Quadrates gelegt. Doch wenn ich naiv den Sketch wie folgt erweitere:

for _ in range(12):
    translate(200, 0)
    rotate(radians(t))
    rect(0, 0, 50, 50)
    rotate(radians(360/12))

Dann fliegen mir die Quadrate sprichwörtlich um die Ohren und rotieren nicht mehr im Kreis, den jedes translate() in der Schleife verschiebt noch einmal den Ursprung der letzten Transformation um die neuen Koordinaten. Man muß hier also einen Ausweg finden.

In Processing (Java) hantiert man hier mit einem Stack: Mit pushMatrix() wird die letzte Koordinatentransformation auf dem Stack abgelegt und mit popMatrix() wird sie wieder hervorgeholt. Das funktioniert auch in Processing.py, ist aber – da man die Codezeilen zwischen push und pop nicht einrücken kann – nicht sehr »pythonisch«. Daher hat man für Processing.py ein eigenes Konstrukt entwickelt, das with-Statement:

    for _ in range(12):
        with pushMatrix():
            translate(200, 0)
            rotate(radians(2*t))
            rect(0, 0, 50, 50)
        rotate(radians(360/12))

Die eingerückten Zeilen hinter with PushMatrix() arbeiten auf dem neuen Koordinatensystem, während das letzte rotate() wieder auf das ursprüngliche Koordinatensystem zugreift. Und alles schön eingerückt, wie wir Pythonistas das lieben und gewohnt sind.

Das kann man auch beliebig wiederholen, wie der vollständige Sketch zeigt:

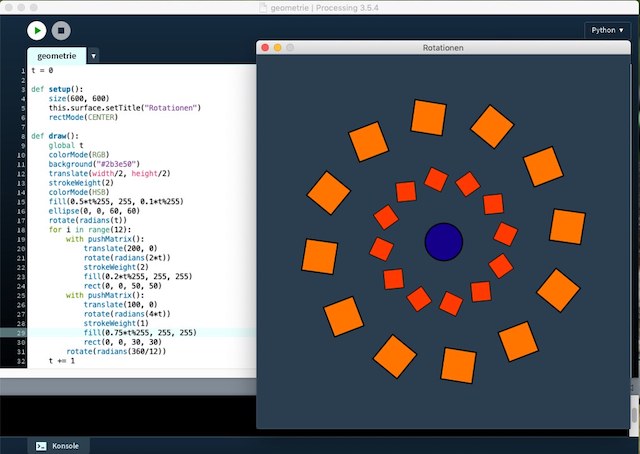
t = 0

def setup():
    size(600, 600)
    this.surface.setTitle("Rotationen")
    rectMode(CENTER)

def draw():
    global t
    colorMode(RGB)
    background("#2b3e50")
    translate(width/2, height/2)
    strokeWeight(2)
    colorMode(HSB)
    fill(0.5*t%255, 255, 0.1*t%255)
    ellipse(0, 0, 60, 60)
    rotate(radians(t))
    for _ in range(12):
        with pushMatrix():
            translate(200, 0)
            rotate(radians(2*t))
            strokeWeight(2)
            fill(0.2*t%255, 255, 255)
            rect(0, 0, 50, 50)
        with pushMatrix():
            translate(100, 0)
            rotate(radians(4*t))
            strokeWeight(1)
            fill(0.75*t%255, 255, 255)
            rect(0, 0, 30, 30)
        rotate(radians(360/12))
    t += 1

In diesem letzten Beispiel rotieren zwei Kreise von je 12 Quadraten mit unterschiedlichen Geschwindigkeiten je Kreis um einen Kreis im Mittelpunkt (siehe Screenshot). Die Farben ändern sich in Abhängigkeit von t (ebenfalls in unterschiedlichen Geschwindigkeiten (x*t) je Kreis). Zwei Stacks sorgen dafür, daß der äußere und der innere Kreis von Quadraten jeweils in seinen eigenen Koordinatensystemen lebt.

Wenn Ihr diesen Sketch laufen laßt, kommt schon fast ein psychedelisches Feeling auf. Vergeßt darüber aber bitte nicht, wie man translate() und rotate() einsetzt. Denn das wollte ich Euch in diesem Tutorial zeigen.

(Kommentieren)