Simulationen mit Processing.py: Fourierreihe

Als Fourierreihe, nach Joseph Fourier (1768–1830), bezeichnet man die Reihenentwicklung einer periodischen, abschnittsweise stetigen Funktion in eine Funktionenreihe aus Sinus- und Kosinusfunktionen. Sie kann unter anderem dazu dienen, verschiedene Pulssignale (zm Beispiel Dreieckpuls, Rechteckpuls oder Sägezahnpuls) mit Sinus- und Kosinustermen zu approximieren. Die drei oben genannten Schwingungen gehören zu den Grundformen der Klangerzeugung bei Synthezisern und elektronischen Orgeln. Daher möchte ich in diesem Beitrag zeigen, wie man eine Fourierreihe erzeugt, die eine Rechteckschwingung approximiert.

Um die Funktionsweise einer Fourierreihe verständlich zu machen, fange ich mit der einfachsten Form an und transformiere einen Kreis von kartesischen Koordinaten in Polarkoordinaten. Die Gleichung dafür lautet bekanntlich

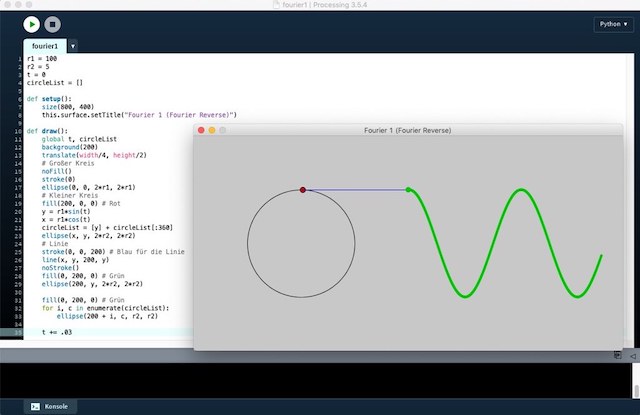
und die im Screenshot unten veranschaulichte Bedeutung dieser Gleichung möchte ich als erstes programmieren.

Dazu zeichne ich als erstes einen Kreis und einen kleinen roten Punkt, der den Umfang des Kreises umlaufen soll:

r1 = 100
r2 = 5
t = 0

def setup():
    size(800, 400)
    this.surface.setTitle("Fourier 1 (Fourier Sinus)")

def draw():
    global t
    background(200)
    translate(width / 4, height / 2)

    # Großer Kreis
    noFill()
    stroke(0)
    ellipse(0, 0, 2 * r1, 2 * r1)

    # Kleiner Kreis
    fill(200, 0, 0)  # Rot
    y = r1 * sin(t)
    x = r1 * cos(t)

    t += 0.02

Der kleine rote Kreis läuft nun unermüdlich um den Kreisbogen herum. Doch nun möchte ich zeigen, daß dies tatsächliche eine Sinusbewegung ist. Dazu habe ich als erstes im Kopf des Programms mit

circleList = []

eine Liste initialisiert und sie in der draw()-Funktion ebenfalls als global erklärt. Diese List wird nun bei jedem Durchlauf mit den y-Wert des kleien roten Kreises verlängert. Damit die Liste nicht ins Unendliche wächst, benutze ich einen kleinen Trick der Listen-Addition:

circleList = [y] + circleList[:360]

Der Slice sorgt dafür, daß die circleList nie mehr als 361 Elemente enthält (zu Beginn des Programms natürlich weniger, bis sie auf 360 Elemente aufgefüllt ist).

Einen weiteren Trick, der den Sketch mehr pythonisch macht, habe ich angewandt, in dem ich Pythons eingebaute enumerate()Funktion verwendet habe. Diese liefert den Index und den Wert des jeweiligen Elements zurück:

    for i, c in enumerate(circleList):
        ellipse(200 + i, c, 3, 3)

Schließlich habe ich der Simualtion noch eine Linie vom Mittelpunkt des großen Kreises zu Mittelpunkt des kleinen Kreises spendiert und eine blaue Linie von den Koordinaten des kleinen Kreises zu einer 200 Pixel in der x-Achse vom Ursprung des Koordinatenssystems entfernt liegenden Stelle im Fenster in der die Sinuskurve gezeichnet werden soll. Der vollständige Sketch sieht daher so aus:

r1 = 100
r2 = 5
t = 0
circleList = []

def setup():
    size(800, 400)
    this.surface.setTitle("Fourier 1 (Fourier Sinus)")

def draw():
    global t, circleList
    background(200)
    translate(width / 4, height / 2)

    # Großer Kreis
    noFill()
    stroke(0)
    ellipse(0, 0, 2 * r1, 2 * r1)

    # Kleiner Kreis
    fill(200, 0, 0)  # Rot
    y = r1 * sin(t)
    x = r1 * cos(t)
    circleList = [y] + circleList[:360]
    ellipse(x, y, 2 * r2, 2 * r2)

    # Linie vom großen zum kleinen Kreis
    line(0, 0, x, y)

    # Linie
    stroke(0, 0, 200)  # Blau für die Linie
    line(x, y, 200, y)
    noStroke()
    fill(0, 200, 0)  # Grün
    ellipse(200, y, 2 * r2, 2 * r2)

    fill(0, 200, 0)  # Grün
    for i, c in enumerate(circleList):
        ellipse(200 + i, c, 3, 3)

    t += .02

Doch wie erreiche ich nun, daß aus dieser einfachen Sinuskurve eine Forierreihe wird, die eine Rechteckschwinung approximiert. Eigentlich ist erstaunlich wenig zu ändern. Zu Beginn habe ich zwei zusätzliche Konstanten initialisiert:

p = 10 # Periode
offset = 250

p ist die Periode der Fourierreihe. Je höher die Periode, desto genauer ist die Approximation. p = 10 erzeugt die Kurve des Screenshots im Kopf dieses Beitrags. Die Approximation ist noch nicht sehr genau, aber bei p = 50 entspricht jede Phase schon fast einer Rechteckschwingung. Und auch bei p = 100 konnte ich selbst auf meinem betagten Macbook Pro keine Performance-Einbußen feststellen.

offset ist einfach eine Konstante für die Koordinatenverschiebung. Da ich ein wenig mit der Position des Nullpunktes der x-Achse experimentieren mußte, um ein vernünftig positioniertes Bild zu erhalten und ich diese Position mehrmals im Programm benötigte, habe ich sie im Kopf des Sketches deklariert.

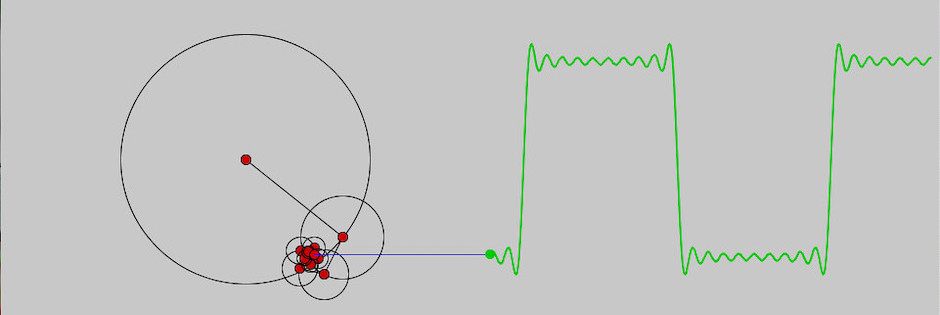
Anschaulich kann man sich ein Fourierreihe so vorstellen, daß auf den großen Kreis an der Position des roten Punktes ein kleinerer Kreis gesetzt wird der ebenfalls von einem roten Punkt umrundet wird und an der Position dieses roten Punktes wieder ein noch kleinerer Kreis, der ebenfalls von einem roten Punkt umrundet wird und so weiter und so fort, bis die festgelegte Periodenzahl erreicht ist.

In Code gegossen, sieht das so aus:

    x = 0
    y = 0
    strokeWeight(1)
    for i in range(p):
        prevx = x
        prevy = y
        
        n = i * 2 + 1
        r1 = 100 * (4 / (n * PI))
        x += r1 * cos(n * t)
        y += r1 * sin(n * t)

        # Großer Kreis
        noFill()
        stroke(0)
        ellipse(prevx, prevy, 2 * r1, 2 * r1)

        # Linie vom großen zum kleinen Kreis
        line(prevx, prevy, x, y)

        # Kleiner Kreis
        fill(200, 0, 0)  # Rot
        ellipse(prevx, prevy, 2 * r2, 2 * r2)
    
    circleList = [y] + circleList[:450]

Im englischsprachigen Wikipedia-Artikel zu den Fourier-Reihen wird die Fourierreihe mit folgendem Term beschrieben,

wobei $i$ nur die ungeraden Zahlen $1, 3, … , p$ durchläuft. Das habe ich mit

n = i * 2 + 1

sichergestellt. Diese neuen Radii müssen jeweils auf den vorhergehenden Kreis aufaddiert werden, dazu müssen aber die vorherigen (x, y)-Koordinaten bekannt sein (prevx, prevy).

Da die Flanken der Kurve zu steil wurden, habe ich die Approximation nicht mehr mit kleinen Punkten gezeichnet, sondern mit

    with beginShape():
        noFill()
        strokeWeight(2)
        stroke(0, 200, 0) # Grün
        for i, c in enumerate(circleList):
            vertex(offset + i, c)

eine durchgehende Linie zeichnen lassen. Der vollständige Sketch, der für den Screenshot im Kopf dieses Beitrages verantwortlich ist, sieht daher so aus:

t = 0
r2 = 5
p = 10 # Periode
offset = 250
circleList = []

def setup():
    size(960, 400)
    this.surface.setTitle("Fourier 2 (Fourier-Reihe)")

def draw():
    global t, circleList
    background(200)
    translate(offset, height / 2)

    x = 0
    y = 0
    strokeWeight(1)
    for i in range(p):
        prevx = x
        prevy = y
        
        n = i * 2 + 1
        r1 = 100 * (4 / (n * PI))
        x += r1 * cos(n * t)
        y += r1 * sin(n * t)

        # Großer Kreis
        noFill()
        stroke(0)
        ellipse(prevx, prevy, 2 * r1, 2 * r1)

        # Linie vom großen zum kleinen Kreis
        line(prevx, prevy, x, y)

        # Kleiner Kreis
        fill(200, 0, 0)  # Rot
        ellipse(prevx, prevy, 2 * r2, 2 * r2)
    
    circleList = [y] + circleList[:450]
    
    # Linie
    fill(200, 0, 0)
    ellipse(x, y, 2 * r2, 2 * r2)
    stroke(0, 0, 200) # Blau für die Linie
    line(x, y, offset, y)
    noStroke()
    fill(0, 200, 0) # Grün
    ellipse(offset, y, 2*r2, 2*r2)
    
    with beginShape():
        noFill()
        strokeWeight(2)
        stroke(0, 200, 0) # Grün
        for i, c in enumerate(circleList):
            vertex(offset + i, c)

    t += .02

Die initiale Idee zu diesem Beitrag kam mir durch den Abschnitt »Make Sine Waves« aus dem schon mehrfach erwähnten Buch »Math Adventures with Python« von Peter Farrell (Seite 110ff), zum Aufbohren der Sinuskurve zu einer Fourierreihe wurde ich durch David Shiffmans Coding Challenge zu Fourierreihen inspiriert, in der er ähnliches in P5.js, dem JavaScript-Mode von Processing programmierte.

Ich selber habe bei diesen Sketchen natürlich wieder auf Processing.py, den Python-Mode von Processing zurückgegriffen. Pythons Listen-Funktionen sind einfach stark und das with-Statement finde ich immer noch genial. Ich hoffe, Ihr merkt meine Begeisterung darüber auch diesen Code-Beispielen an.

Links

Neben den schon verlinkten Beiträgen habe ich auch auf folgende Quellen, die in der Hauptsache aus Shiffmans Coding Challenge stammen, zurückgegriffen:

– Purrier Series (Meow) and Making Images Speak, Bilim Ne Güzel Lan! (beta) vom 11. Dezember 2018 - An Interactive Guide To The Fourier Transform, Better Explained - Video: Was ist eine Fourierreihe? (englisch) - Video: Doch was ist eine Fourier-Transformation? (englisch)

Den Quellcode zu den beiden Sketchen könnt Ihr – wie üblich – in meinem GutHub-Repositorium finden Fourier 1 und Fourier 2.

(Kommentieren)