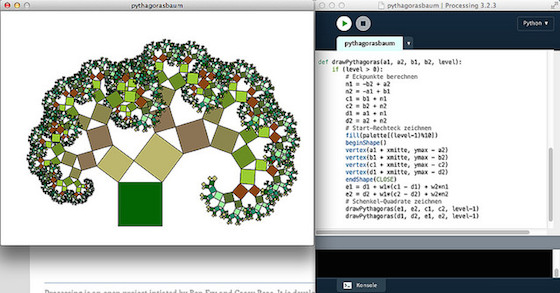
Wochenendspaß mit Processing.py: Der Baum des Pythagoras

Eine weitere Ikone der fraktalen Geometrie ist der Pythagoras-Baum. Er geht zurück auf den niederländischen Ingenieur und späteren Mathematiklehrer Albert E. Bosman (1891–1961). Er entwarf während des 2. Weltkrieges in seiner Freizeit an einem Zeichenbrett, an dem er sonst U-Boot-Pläne zeichnete, geometrische Muster. Seine Graphiken wurden 1957 in dem Buch »Het wondere onderzoekingsveld der vlakke meetkunde« veröffentlicht.

Der Pythagoras-Baum beruht auf einer rekursiven Abbildung des Pythagoras-Lehrsatzes: Die beiden Quadrate auf den Katheten des rechtwinkligen Dreiecks dienen als Verzweigung, auf dem jedes Kathetenquadrat sich wiederum verzweigt.

Die Funktion drawPythagoras

Um die Funktion rekursiv aufrufen zu können, mußte ich sie aus der draw()-Funktion auslagern und sie in einen eigenen Aufruf packen:

def drawPythagoras(a1, a2, b1, b2, level):
    if (level > 0):
        # Eckpunkte berechnen
        n1 = -b2 + a2
        n2 = -a1 + b1
        c1 = b1 + n1
        c2 = b2 + n2
        d1 = a1 + n1
        d2 = a2 + n2
        # Start-Rechteck zeichnen
        fill(palette[(level-1)%10])
        with beginClosedShape():
            vertex(a1 + xmitte, ymax - a2)
            vertex(b1 + xmitte, ymax - b2)
            vertex(c1 + xmitte, ymax - c2)
            vertex(d1 + xmitte, ymax - d2)
        e1 = d1 + w1*(c1 - d1) + w2*n1
        e2 = d2 + w1*(c2 - d2) + w2*n2
        # Schenkel-Quadrate zeichnen
        drawPythagoras(e1, e2, c1, c2, level-1)
        drawPythagoras(d1, d2, e1, e2, level-1)

Zum Zeichnen der einzelnen Quadrate habe ich nicht die rect()-Funktion genutzt, sondern Shapes, mit denen sich Punkte zu einem beliebigen Gebilde oder Polygon zusammefassen lassen. Hierzu müssen sie erst einmal mit with beginClosedShape() geklammert werden. Darin werden dann mit vertex(x, y) nacheinander die einzelnen Punkt aufgerufen, die (im einfachten Fall) durch Linien miteinander verbunden werden sollen. Mit beginClosedShape teile ich dem Sketch auch mit, daß das entstehende Polygon auf jeden Fall geschlossen werden soll, ein einfaches with beginShape() würde es offen lassen.

Der Aufruf ist rekursiv: Nachdem zuerst das Grundquadrat gezeichnet wurde, werden die rechten und die linken Schenkelquadrate gezeichnet, die dann wieder als Grundquadrate für den nächsten Rekursionslevel fungieren.

Processing (und damit auch der Python-Mode von Processing) ist gegenüber Rekursionstiefen realtiv robust. Die benutzte Rekursionstiefe von 12 wird klaglos abgearbeitet, auch Rekursionstiefen bis 20 sind – genügend Geduld vorausgesetzt – kein Problem. Bei einer Rekursionstiefe von 22 verließ mich aber auf meinem betagten MacBook Pro die Geduld.

Die Farben

Für die Farben habe ich eine Palette in einer Liste zusammengestellt, die der Reihe nach die Quadrate einfärbt. Da die Liste nur 10 Elemente enthält, habe ich mit fill(palette[(level-1)%10]) dafür gesorgt, daß nach zehn Leveln die Palette wieder von vorne durchlaufen wird.

Der Quellcode

Da die eigentliche Aufgabe des Programms in die Funktion drawPythagoras() ausgelagert wurde, ist der restlich Quellcode von erfrischender Kürze:

palette = [color(189,183,110), color(0,100,0), color(34,139,105),
           color(152,251,152), color(85,107,47), color(139,69,19),
           color(154,205,50), color(107,142,35), color(139,134,78),
           color(139, 115, 85)]

xmax = 600
xmitte = 300
ymax = 440

level = 12
w1 = 0.36   # Winkel 1
w2 = 0.48   # Winkel 2

def setup():
    size(640, 480)
    background(255)
    strokeWeight(1)
    noLoop()

def draw():
    drawPythagoras(-(xmax/10), 0, xmax/20, 0, level)

def drawPythagoras(a1, a2, b1, b2, level):
    if (level > 0):
        # Eckpunkte berechnen
        n1 = -b2 + a2
        n2 = -a1 + b1
        c1 = b1 + n1
        c2 = b2 + n2
        d1 = a1 + n1
        d2 = a2 + n2
        # Start-Rechteck zeichnen
        fill(palette[(level-1)%10])
        with beginClosedShape():
            vertex(a1 + xmitte, ymax - a2)
            vertex(b1 + xmitte, ymax - b2)
            vertex(c1 + xmitte, ymax - c2)
            vertex(d1 + xmitte, ymax - d2)
        e1 = d1 + w1*(c1 - d1) + w2*n1
        e2 = d2 + w1*(c2 - d2) + w2*n2
        # Schenkel-Quadrate zeichnen
        drawPythagoras(e1, e2, c1, c2, level-1)
        drawPythagoras(d1, d2, e1, e2, level-1)

Auch wenn es nicht nötig gewesen wäre, ich mag es einfach (und es dient der Übersichtlichkeit), wenn ich meine Processing.py-Sketche mit def setup() und def draw() gliedere. Mit noLoop() habe ich dann dafür gesorgt, daß die draw()-Schleife nur einmal abgearbeitet wird.

Erweiterungen und Änderungen

Einen »symmetrischen« Pythagoras-Baum erhält man übrigens, wenn man die beiden Winkel-Konstanten w1 und w2 jeweils auf 0.5 setzt.

Credits

Den rekursiven Algorithmus habe ich einem Pascal-Programm aus Jürgen Plate: Computergrafik: Einführung – Algorithmen – Programmentwicklung, München (Franzis) 2. Auflage 1988, Seiten 460-462 entnommen. Und die Geschichte des Baumes steht in dem schon mehrfach erwähnten Buch von Dieter Hermann, Algorithmen für Chaos und Fraktale, Bonn (Addison-Wesley) 1944 auf den Seiten 170f.

Auch diesen Beitrag habe ich auf meine stetig wachsende Site »Processing.py lernen« hochgeladen, die nun schon einen beachtlichen Umfang angenommen hat. Änderungen, Ergänzungen und/oder Fehlerkorrekturen wird es nur dort geben.

---

(Kommentieren)