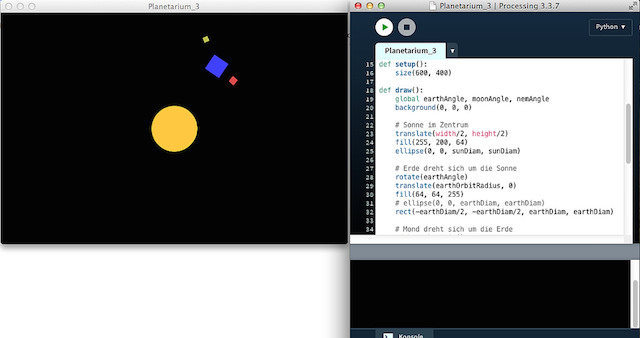
Tutorial: Ein kleines Planetensystem in Processing.py

Als Projekt für mein geplantes Processing.py-Buch möchte ich eine kleine Animation eines Planetensystems aus Kreisen und Rechtecken entwickeln. Ich weiß, Planeten sind kugelförmig und keine Kisten, aber in der virtuellen Welt von Processing ist alles möglich. Außerdem möchte ich damit zeigen, wie nützlich die Transformationsoperatoren translate() und rotate() sein können und dafür brauche ich die Rechtecke zur Verdeutlichung.

Ich beginne mit einem einfachem System eines Planeten, der seinen Fixstern umkreist, und dieser besitzt einen Trabanten, der wiederum den Planeten umreist. Der Einfachheit halber habe ich die Akteure Sonne, Erde und Mond genannt.

Zu Beginn des Sketches lege ich erst einmal ein paar Zahlen fest:

sunDiam = 80

earthDiam = 30
earthOrbitRadius = 130
earthAngle = 0

moonDiam = 10
moonOrbitRadius = 50
moonAngle = 0

Diese Zahlen sind durch keine physikalische Wirklichkeit gedeckt, sondern einfach so lange durch Experimente herausgesucht worden, bis sich eine ansprechende Animation ergab.

Die setup()-Funktion legt einfach nur die Größe des Ausgabefensters fest:

def setup():
    size(600, 400)

In draw() setze ich den Hintergrund auf schwarz und dann zeichne ich die Sonne in die Mitte des Ausgabefensters:

def draw():
    global earthAngle, moonAngle
    background(0, 0, 0)
    
    # Sonne im Zentrum
    translate(width/2, height/2)
    fill(255, 200, 64)
    ellipse(0, 0, sunDiam, sunDiam)

Die Zeile translate(width/2, height/2) sorgt dafür, daß der Nullpunkt des Koordinatensystem vom linken oberen Rand in die Mitte des Ausgabefensters gelegt wird und so die Sonne mit ellipse(0, 0, sunDiam, sunDiam) auch genau dort gezeichnet wird. Probiert es aus, der Sketch ist so lauffähig.

Die beiden Variablen earthAngle und moonAngle sind die beiden einzigen Variablen, die sich später in der draw()-Funktion noch ändern werden, daher mußten sie als global definiert werden.

Nun zur Erde, die die Sonne umkreist:

    # Erde dreht sich um die Sonne
    rotate(earthAngle)
    translate(earthOrbitRadius, 0)
    fill(64, 64, 255)
    ellipse(0, 0, earthDiam, earthDiam)
    
    earthAngle += 0.01

Wenn Ihr diese Zeilen Code in die draw()-Funktion unterhalb der Sonne einfügt, bekommt Ihr eine blaue Erde, die sich langsam um die Sonne bewegt. Denn mit translate(earthOrbitRadius, 0) wurde das Koordinatensystem erneut verschoben, 180 Pixel von der Sonne entfernt aber auf der gleichen y-Achse wie das Koordinatensystem der Sonne. Da rotate() vor der Koordinatentransformation aufgerufen wird, dreht sich die Erde noch um die Sonne und das Koordinatensystem der Sonne rotiert, ein rotate() hinter der Koordinatentransformation würde bewirken, daß sich die Erde um sich selbst dreht – das heißt, daß das Koordinatensystem der Erde rotieren würde.

Zum Schluß wird noch der Mond angehängt:

    # Mond dreht sich um die Erde
    rotate(moonAngle)
    translate(moonOrbitRadius, 0)
    fill(192, 192, 80)
    ellipse(0, 0, moonDiam, moonDiam)
    
    moonAngle += 0.01

Durch diese Koordinatentransformation steht der Mond im gleichen Verhältnis zur Erde wie die Erde zur Sonne, der Ursprung des Koordinatensystems liegt nun 50 Pixel vom Erdmittelpunkt entfernt. Natürlich rotiert in diesen Zeilen das Koordinatensystem der Erde, damit der Eindruck entsteht, daß der Mond um die Erde kreist.

Das alles funktioniert natürlich nur, weil bei jedem erneuten Durchlauf der draw()-Funktion das Koordinatensystem zurückgesetzt wird, also alle Transformationen »vergessen« werden.

Nun kann man bei Kreisen schwer erkennen, ob sie wirklich rotieren, daher habe ich in einer zweiten Fassung, die Kreise von Erde und Mond durch Quadrate ersetzt (ich habe – damit Ihr die Position der Codezeilen findet, die ersetzte Kreisfunktion jeweils auskommentiert stehen lassen, die Rechteckfunktion wird jeweils direkt unter der auskommentierten Zeile eingefügt):

    # ellipse(0, 0, earthDiam, earthDiam)
    rect(-earthDiam/2, -earthDiam/2, earthDiam, earthDiam)
    …
    # ellipse(0, 0, moonDiam, moonDiam)
    rect(-moonDiam/2, -moonDiam/2, moonDiam, moonDiam)

Wenn Ihr das Programm jetzt startet, dreht sich eine große blaue Kiste um die Sonne mit einer kleinen grauen Kiste, die sich um die Erde dreht und Ihr könnt die Rotation der beiden Kisten genau beobachten.

Doch was ist, wenn ein zweiter Mond – nennen wir ihn Nemesis – um die Erde kreisen soll? Das Koordinantensystem der Erde ist ja schon vom Koordinatensystem des Mondes ersetzt worden. Wir brauchen also eine Funktion, die das Koordinatensystem nur temporär verschiebt, so daß man auf das alte Koordinatensystem wieder zrückgreifen kann, wenn es benötigt wird. Genau dafür gibt es in Processing das Funktionenpaar pushMatrix() und popMatrix(). Mit pushMatrix() wird das bisherige Koordinatensystem auf einen Stack gelegt und mit popMatrix() wird es wieder zurückgeholt. Und in Processing.py gibt es noch, wie ich hier gezeigt hatte, eine besondere Möglichkeit, nämlich das width-Statement, die das jeweilige popMatrix() überflüssig macht: Solange der Code unter dem with-Statement eingerückt ist, wird mit den neuen Koordinaten des width-Statements gearbeitet, wird der Code wieder ausgerückt, werden die auf den Stack gelegten Koordinaten zurückgeholt.

Erst einmal braucht natürlich Nemesis seinen eigenen Satz Variablen,

nemDiam = 12
nemOrbitRadius = 38
nemAngle = 0

wobei nemAngle analog zu den anderen Winkeln zu Beginn der draw()-Schleife als global definiert werden muß:

    global earthAngle, moonAngle, nemAngle

Und dann habe ich Nemesis und dem Mond jeweils eine eigene (Koordinaten-) Matrix spendiert

    # Mond dreht sich um die Erde
    with pushMatrix():
        rotate(moonAngle)
        translate(moonOrbitRadius, 0)
        fill(192, 192, 80)
        # ellipse(0, 0, moonDiam, moonDiam)
        rect(-moonDiam/2, -moonDiam/2, moonDiam, moonDiam)
    
    # Nemesis dreht sich um die Erde
    with pushMatrix():
        rotate(nemAngle)
        translate(nemOrbitRadius, 0)
        fill(220, 75, 75)
        # ellipse(0, 0, nemDiam, nemDiam)
        rect(-nemDiam/2, -nemDiam/2, nemDiam, nemDiam)

und zum Schluß nemAngle um 0.015 inkrementiert. Das gesamte Programm sieht nun so aus:

sunDiam = 80

earthDiam = 30
earthOrbitRadius = 130
earthAngle = 0

moonDiam = 10
moonOrbitRadius = 50
moonAngle = 0

nemDiam = 12
nemOrbitRadius = 38
nemAngle = 0

def setup():
    size(600, 400)

def draw():
    global earthAngle, moonAngle, nemAngle
    background(0, 0, 0)
    
    # Sonne im Zentrum
    translate(width/2, height/2)
    fill(255, 200, 64)
    ellipse(0, 0, sunDiam, sunDiam)
    
    # Erde dreht sich um die Sonne
    rotate(earthAngle)
    translate(earthOrbitRadius, 0)
    fill(64, 64, 255)
    # ellipse(0, 0, earthDiam, earthDiam)
    rect(-earthDiam/2, -earthDiam/2, earthDiam, earthDiam)
    
    # Mond dreht sich um die Erde
    with pushMatrix():
        rotate(moonAngle)
        translate(moonOrbitRadius, 0)
        fill(192, 192, 80)
        # ellipse(0, 0, moonDiam, moonDiam)
        rect(-moonDiam/2, -moonDiam/2, moonDiam, moonDiam)
    
    # Nemesis dreht sich um die Erde
    with pushMatrix():
        rotate(nemAngle)
        translate(nemOrbitRadius, 0)
        fill(220, 75, 75)
        # ellipse(0, 0, nemDiam, nemDiam)
        rect(-nemDiam/2, -nemDiam/2, nemDiam, nemDiam)
        
    earthAngle += 0.01
    moonAngle += 0.01
    nemAngle += 0.015

Natürlich hätte man die Nemesis betreffenden Zeilen nicht in eine eigenes width-Statement klammern müssen, aber so ist es auberer und Ihr könnt der Erde noch einen dritten und einen vierten Trabanten spendieren, ohne mit den Koordinatensystemen durcheinander zu kommen.

Wenn Ihr das Programm laufen laßt, werdet Ihr sehen, warum ich für die Erde und ihre Trabanten Rechtecke gewählt habe. So ist zu erkennen, daß die Erde mit genau einer Seite immer zur Sonne zeigt und die beiden Trabanten ebenfalls mit genau einer Seite zur Erde. Das ist, weil sie sich jeweils in ihrem eigenen Koordinatensystem bewegen, dessen eine Achse immer das Zentrum des darüberliegenden Koordinatensystems schneidet.

Für die Monde ist das okay, wenn Ihr der Erde aber Tag und Nacht spendieren wollt, müßt Ihr ihr noch ein zweites rotate() nach der Koordinatentransformation spendieren.

Natürlich ist das Progrämmchen ausbaubar. Ihr könnt mehrere Planeten jeweils mit ihren eigenen Koordinatensystemen um den Fixstern kreisen lassen. Alle diese Planeten könnt Ihr mit Monden umgeben, die wiederum ihr eigenes Koordinatensystem besitzen. Und wenn Ihr wirkliche Helden sein wollt: Schnappt Euch ein Buch mit den Keplerschen Gesetzen zur Planetenbewegung und simuliert damit ein realistischeres Planetensystem.

Literatur

Die Idee zu diesem Sketch und einige der Parameter habe ich dem wunderbaren Buch »Processing for Visual Artists – How to Create Expressive Images and Interactive Art« von Andrew Glassner (Natick, MA, 2010), Seiten 192-200 entnommen und von Java nach Python portiert.

---

(Kommentieren)