Spaß mit Polarkoordinaten (und Processing.py): Primzahlspirale

Es gibt eigentlich keinen vernünftigen und nachvollziehbaren Grund, Primzahlen ($p$) in Polarkoordinaten in der Form $(\rho, \theta) = (p, p)$ darzustellen, aber erstens brauchen Mathematiker nie einen vernünftigen und nachvollziehbaren Grund und zweitens kann es überraschenderweise dennoch zu einem Erkenntnisgewinn führen. Doch dazu später mehr (aus berufenerem Mund als meinen), ich habe mir erst einmal angeschaut, wie man diese Darstellung in Processing.py programmiert und wie das Ergebnis aussehen kann:

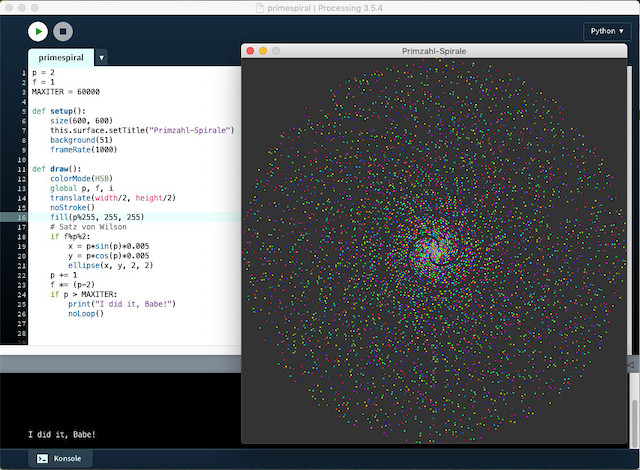
Bekanntlich wird ja in vielen Programmiersprachen (und so auch in Processing) bei den Winkelfunktionen der Parameter im Bogenmaß (Radiant) $(0 < 2\pi) %$ angegeben und nicht in Grad. Das ist in diesem Falle von Vorteil, denn einmal erspart es uns die Umrechnung und zum anderen liefert es uns eine Erklärung für die spiralförmigen Strukturen, die in diesem Screenshot zu sehen sind. Doch erst einmal das vollständige Programm:

p = 2
f = 1
MAXITER = 60000

def setup():
    size(600, 600)
    this.surface.setTitle("Primzahl-Spirale")
    background(51)
    frameRate(1000)
        
def draw():
    colorMode(HSB)
    global p, f, i
    translate(width/2, height/2)
    noStroke()
    fill(p%255, 255, 255)
    # Satz von Wilson
    if f%p%2:
        x = p*sin(p)*0.005
        y = p*cos(p)*0.005
        ellipse(x, y, 2, 2)
    p += 1
    f *= (p-2)
    if p > MAXITER:
        print("I did it, Babe!")
        noLoop()    

Interessant ist eigentlich nur die Zeile

    if f%p%2:

Denn diese liefert die Prüfung, ob eine Zahl prim ist in der kompaktesten Form, die ich kenne. Es ist eine Umformulierung des Satzes von Wilson:

Sei $p \ge 2$ eine natürliche Zahl. Dann ist $p$ genau dann eine Primzahl, wenn $(p-1)! + 1$ durch $p$ teilbar ist.

Seit meinem (schon lange zurückliegendem) Mathematikstudium hasse ich eigentlich die in Mathematik(lehr)büchern übliche Formulierung »wie man leicht sieht«. Aber wenn man sich die obige Programmzeile und die Entwicklung f *= (p-2) lange genug anschaut, dann erkennt man tatsächlich (wenn auch nicht gerade leicht), daß dies tatsächlich eine ziemlich geniale Anwendung des Satzes von Wilson ist¹.

Der Satz von Wilson ist nicht so effektiv (so schnell) wie andere klassische Alogrithmen, wie zum Beispiel das Sieb des Eratosthenes, aber ich war von der Kompaktheit so fasziniert, das ich ihn genommen habe (für meine kleine Anwendung reicht er völlig aus).

Was bedeuten nun diese Spiral-Patterns und – vor allen Dingen – was bedeuten die Lücken zwischen den Spiralen, die sich bei einer noch größeren Primzahl-Obergrenze scheinbar zu Strahlen entwickeln. Diese Frage beantwortet (kompetenter als ich es je könnte) 3Blue1Brown in obigen Video. Es hat etwas damit zu tun, daß zum Beispiel $44 rad$ eine ziemlich gute und $710 rad$ eine fast perfekte Näherung für $2\pi$ sind. Das führt Euch dann zum Dirichletschen Primzahlsatz und zum Totienten der Eulerschen $\phi$-Funktion.

Ihr seht also: Auch wenn man einfach etwas nur aus Spielerei und ohne vernünftigen und nachvollziehbaren Grund probiert, kann es zu weitreichenden Erkenntnissen führen. Das ist das, was mich seit meinem Abitur am Berlin Kolleg (mit großem Dank an meinen Mathematiklehrer Dr. Hugo Sachs) an Mathematik bis heute fasziniert.

Caveat

Diese Primzahlspirale ist nur indirekt mit der auch häufig als (quadratische) Primzahlspirale bezeichneten Ulam-Spirale verwandt. Neben anderen hat sie aber eine Gemeinsamkeit: Sie entstand, als sich der polnische Mathematiker Stanisław Marcin Ulam während eines wissenschaftlichen Vortrages so langweilte, daß er die natürlichen Zahlen nach einem quadratischen Muster auf kariertes Papier notierte und dann die Primzahlen markierte. Prompt fielen ihm regelmäßige Strukturen auf (die Primzahlen befanden sich häufiger auf Diagonalen und Geraden), die er weiter untersuchen mußte. Auch hier gab es keinen vernünftigen und nachvollziehbaren Grund, warum Ulam ausgerechnet diese Darstellung der Primzahlen wählte, aber … das Muster der Ulam-Spirale kann bis heute nicht vollständig erklärt werden.

(Kommentieren)