»Autonome Agenten« in Processing.py

Schockwellenreiter → Archiv → September 2020 → »Autonome Agenten« in Python (Processing) – 20200922

»Autonome Agenten« in Processing.py

In diesem und weiteren (Programmier-) Experimenten möchte ich mich dem Themenkomplex »Autonome Agenten« mit Processing.py, dem Python-Mode von Processing. annähern. Ich beziehe mich dabei zum einen auf das sechste Kapitel von Daniel Shiffmans Buch »The Nature of Code«, wie auch auf das darin erwähnte Bändchen »Vehikel. Experimente mit kybernetischen Wesen« von Valentin Braitenberg, der von 1968 bis zu seiner Emeritierung 1994 Direktor am Max-Planck-Institut für biologische Kybernetik in Tübingen war.

Den Begriff »Autonome Agenten« habe ich in Anführungszeichen gesetzt, weil die »Viehicle«¹ in den Simulationen nicht wirklich autonom sind, sondern nur autonom erscheinen.

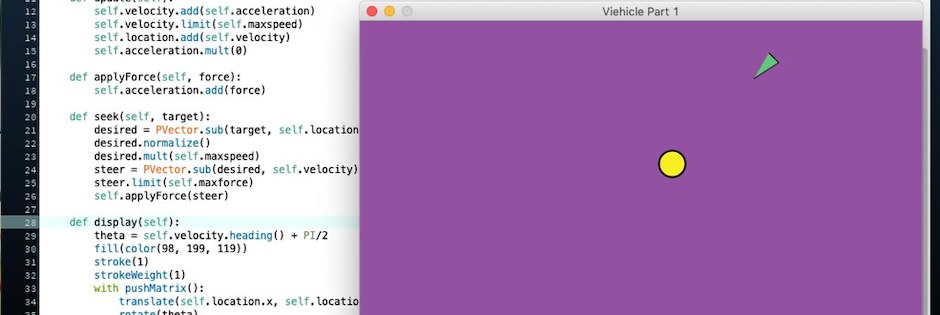
In einer ersten Simulation möchte ich einen »Agenten« programmieren, der einer gelben Kugel (einer Sonne) folgt, deren Position wiederum vom Mauszeiger gesteuert wird. Er folgt dabei einem Vektor velocity, der von einem Vektor steer (Lenkverhalten) in die Richtung des Ziels gelenkt wird. Das Ziel (target) wird durch einen Vektor desired beschrieben. Dabei ist desired = target - location, wobei das Lenkverhalten durch die Konstante maxspeed eingeschränkt wird und steer = desired - velocity. In meiner Klasse Viehicle wird dieses Suchverhalten wie folgt modelliert:

    def seek(self, target):
        desired = PVector.sub(target, self.location)
        # Check Boundaries
        if self.location.x < self.d:
            desired = PVector(self.maxspeed, self.velocity.y)
        elif self.location.x > width - self.d:
            desired = PVector(-self.maxspeed, self.velocity.y)
        if self.location.y < self.d:
            desired = PVector(self.velocity.x, self.maxspeed)
        elif self.location.y > height - self.d:
            desired = PVector(self.velocity.x, -self.maxspeed)
        desired.normalize()
        desired.mult(self.maxspeed)
        steer = PVector.sub(desired, self.velocity)
        steer.limit(self.maxforce)
        self.applyForce(steer)

Mit den if … elif-Zeilen hinter # Check Boudaries wird dafür gesorgt, daß der Agent nicht zu weit aus dem Fenster geschleudert wird.

Interessant ist auch noch die display()-Methode, wo der Agent mit einer Konstruktion aus Vertizes als schmales Dreieck gezeichnet wird, dessen Spitze immer in Richtung der Bewegung zeigt:

    def display(self):
        theta = self.velocity.heading() + PI/2
        fill(color(98, 199, 119))
        stroke(1)
        strokeWeight(1)
        with pushMatrix():
            translate(self.location.x, self.location.y)
            rotate(theta)
            with beginShape():
                vertex(0, -self.r*2)
                vertex(-self.r, self.r*2)
                vertex(self.r, self.r*2)

Um dies zu erreichen, werden die Original-Koordinaten erst einmal mit pushMatrix() gesichert, dann wird mit translate ein neues Koordinatensystem mit dem Ursprung im Mittelpunkt des Agenten erzeugt und mit rotate(theta) in die Richtung desngewünschten Zieles gedreht.

Diese Methode zeigt noch einmal die Power, die in der with-Anweisung von Processing.py steckt, denn mit dem Ende der Einrückungen werden die Koordinaten wieder auf den Ursprung zurückgesetzt.

Doch nun den gesamten Quellcode, erst einmal die Klasse Viehicle, die in einem eigenen Reiter untergebracht ist:

class Viehicle():
    
    def __init__(self, x, y):
        self.acceleration = PVector(0, 0)
        self.velocity = PVector(0, 0)
        self.location = PVector(x, y)
        self.r = 8.0
        self.maxspeed = 5
        self.maxforce = 0.1
        self.d = 25
    
    def update(self):
        self.velocity.add(self.acceleration)
        self.velocity.limit(self.maxspeed)
        self.location.add(self.velocity)
        self.acceleration.mult(0)
    
    def applyForce(self, force):
        self.acceleration.add(force)
        
    def seek(self, target):
        desired = PVector.sub(target, self.location)
        # Check Boundaries
        if self.location.x < self.d:
            desired = PVector(self.maxspeed, self.velocity.y)
        elif self.location.x > width - self.d:
            desired = PVector(-self.maxspeed, self.velocity.y)
        if self.location.y < self.d:
            desired = PVector(self.velocity.x, self.maxspeed)
        elif self.location.y > height - self.d:
            desired = PVector(self.velocity.x, -self.maxspeed)
        desired.normalize()
        desired.mult(self.maxspeed)
        steer = PVector.sub(desired, self.velocity)
        steer.limit(self.maxforce)
        self.applyForce(steer)
   
    def display(self):
        theta = self.velocity.heading() + PI/2
        fill(color(98, 199, 119))
        stroke(1)
        strokeWeight(1)
        with pushMatrix():
            translate(self.location.x, self.location.y)
            rotate(theta)
            with beginShape():
                vertex(0, -self.r*2)
                vertex(-self.r, self.r*2)
                vertex(self.r, self.r*2)

Dann das Hauptprogramm, das nur durch die debug-Behandlung² etwas länger als gewohnt geraten ist:

from viehicle import Viehicle

d = 25

def setup():
    global v, debug
    size(640, 360)
    this.surface.setTitle("Viehicle Part 1")
    v = Viehicle(width/2, height/2)
    debug = False
    
def draw():
    global v, debug
    background(color(146, 82, 161))
    
    if debug:
        stroke(175)
        noFill()
        rectMode(CENTER)
        rect(width/2, height/2, width - d*2, height - d*2)
        
    target = PVector(mouseX, mouseY)
    
    fill(color(248, 239, 34))
    stroke(1)
    strokeWeight(2)
    circle(target.x, target.y, 30)
    
    v.seek(target)
    v.update()
    v.display()

def mousePressed():
    global debug
    debug = not debug

Wie immer ist der Quellcode auch in meinem GitHub-Repositorium zu finden.

Literatur

Braitenbergs Vehikel sind in dem oben genannten Buch »Vehikel. Experimente mit kybernetischen Wesen«, Reinbek (rororo) 1993 ausführlich beschrieben.
Ein für diesen Themenbereich ebenfalls interessantes Werk ist der von Valentin Braitenberg und Inga Hosp herausgegebene Sammelband »Simulation. Computer zwischen Experiment und Theorie«, Reinbek (rororo) 1995, der ausgearbeitete Texte des »Bozner Treffens« 1994 enthält.

Bei Braitenberg heißen diese Agenten »Vehicle«, ich vermute, weil sein Buch mit diesem Titel 1984 zuerst in den USA bei MIT Press erschien, mir erscheint »Viehicle« aber ironischer. 🤓 und daher angemessener. ↩
Diese debug-Behandlung zieht nur einen Rahmen, innerhalb dessen der Agent agiert. Zwar schießt er, ja nach maxspeed trotzdem häufig noch über diesen Rahmen heraus, aber er ist die Grenze, hinter der die Kraft nachläßt und der Agent zur Umkehr gezwungen wird. Um damit zu spielen, könnt Ihr mit der Konstante d (die immer mit der Variablen self.d in Viehicle über einstimmen sollte) und den Variablen self.maxspeed und self.maxforce experimentieren. ↩

(Kommentieren)