Worknote: Newton-Fraktale in Processing.py

Mit dem Newton-Verfahren lassen sich die Nullstellen nichtlinearer Gleichungen numerisch approximieren. Die grundlegende Idee dieses Verfahrens ist, die Funktion in einem Ausgangspunkt zu linearisieren, das heißt, ihre Tangente zu bestimmen, und die Nullstelle der Tangente als verbesserte Näherung der Nullstelle der Funktion zu verwenden. Die erhaltene Näherung dient als Ausgangspunkt für einen weiteren Verbesserungsschritt. Diese Iteration erfolgt, bis die Änderung in der Näherungslösung eine festgesetzte Schranke (𝜀) unterschritten hat. Wendet man dieses Verfahren in einer komplexen Umgebung an, erhält man bei mindestens drei Nullstellen immer ein Fraktal, eine Julia👩‍🦰-Menge.

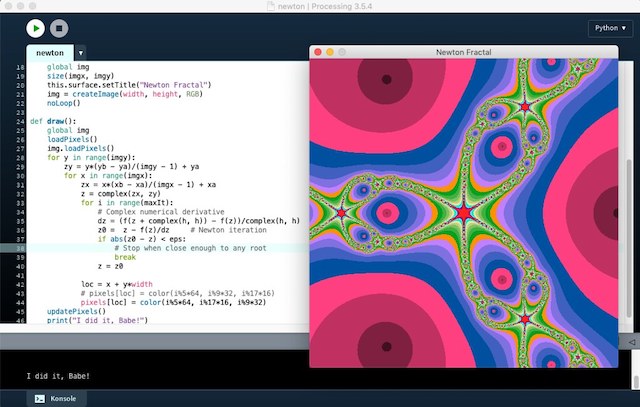
Im Fall von f(z) = z³ - 1 sieht die Julia Menge wie im obigen Screenshot aus. Man sieht deutlich, welche Ausganspunkte immer gegen die (komplexen) Nullstelle streben (rosa), aber auch welche divergieren (rot bis grün). Es gibt unendlich viele divergente Stelle, die von einem anziehenden Zyklus {0, 1} eingefangen werden, aber auch das Newton-Fraktal selber ist nicht beschränkt, es reicht im obigen Beispiel in den drei zu erkennenden Richtungen bis nach ∞.

Die Abbildung wurde mit diesem Processing.py-Sketch erzeugt:

imgx = 512
imgy = 512

# Drawing area
xa = -1.0
xb = 1.0
ya = -1.0
yb = 1.0

maxIt = 20 # max iterations allowed
h = 1e-6   # stepsize for numerical derivative
eps = 1e-3 # max error allowed

def f(z):
    return z*z*z - 1.0

def setup():
    global img
    size(imgx, imgy)
    this.surface.setTitle("Newton Fractal")
    img = createImage(width, height, RGB)
    noLoop()

def draw():
    global img
    loadPixels()
    img.loadPixels()
    for y in range(imgy):
        zy = y*(yb - ya)/(imgy - 1) + ya
        for x in range(imgx):
            zx = x*(xb - xa)/(imgx - 1) + xa
            z = complex(zx, zy)
            for i in range(maxIt):
                # Complex numerical derivative
                dz = (f(z + complex(h, h)) - f(z))/complex(h, h)
                z0 =  z - f(z)/dz     # Newton iteration
                if abs(z0 - z) < eps:
                    # Stop when close enough to any root
                    break
                z = z0
                
            loc = x + y*width
            pixels[loc] = color(i%5*64, i%17*16, i%9*32)
    updatePixels()
    print("I did it, Babe!")

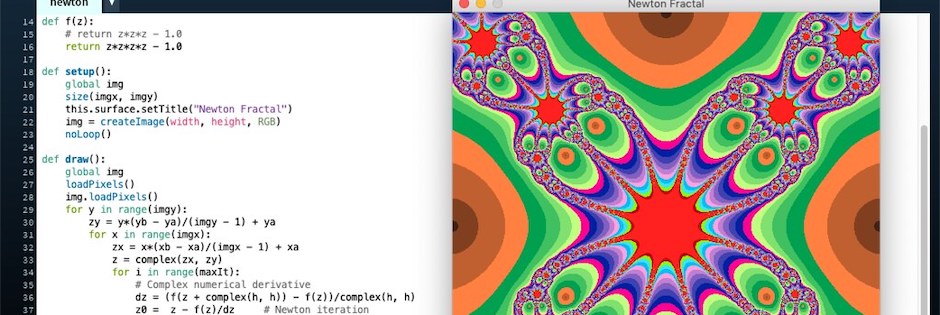
Im Prinzip erzeugt jedes beliebige komplexe Polynom ein Newton-Fraktal. Für die Header-Graphik habe ich die Funktion f(z) = z⁴ - 1 verwendet, die (Überraschung!) natürlich vier Nullstellen besitzt (Screenshot):

def f(z):
    return z*z*z*z - 1.0

Außerdem habe ich eine andere Farbverteilung benutzt:

            pixels[loc] = color(i%5*64, i%9*32, i%17*16)   

Man kann natürlich auch je nach Nullstelle einfärben, also jeder Nullstelle eine Grundfabre zuweisen, die um so heller wird, je schneller der Startwert in der komplexen Ebene gegen 𝜀 konvergiert. Dazu verwendet man in Processing(.py) statt des RGB-Farbraums am Besten den HSB-Farbraum. Wegen meines ziemlich eingeschränkten Farbsehvermögens überlasse ich diese Experimente allerdings der geneigten Leserin oder dem geneigten Leser.

(Kommentieren)