Die Kochsche Schneeflocke – Fraktale mit TigerJythons Turtle

Die Koch-Kurve oder Kochsche Kurve ist ein vom schwedischen Mathematiker Helge von Koch 1904 vorgestelltes Beispiel für eine überall stetige, aber nirgends differenzierbare Kurve. Es handelt sich bei ihr ferner um eines der ersten formal beschriebenen fraktalen Objekte. Die Koch-Kurve ist eines der am häufigsten zitierten Beispiele für ein Fraktal und wurde bei der Entdeckung als Monsterkurve bezeichnet. Heute gehört sie zu den Ikonen der fraktalen Geometrie.

Wenn man drei oder vier Kochkurven im geeigneten Winkel zusammensetzt, erhält man eine Abbildung, die unter dem Namen Kochsche Schneeflocke oder Kochsche Insel bekannt ist. Diese Kochsche Schneeflocke hatte ich vor einigen Jahren schon einmal mit (C) Pythons Turtle programmiert und hier im Blog Kritzelheft vorgestellt. Im Rahmen meiner wachsenden Begeisterung für TigerJython wollte ich nun wissen, wie einfach oder schwierig eine Portierung nach TigerJython ist. Spoiler: Es ist wirklich einfach!

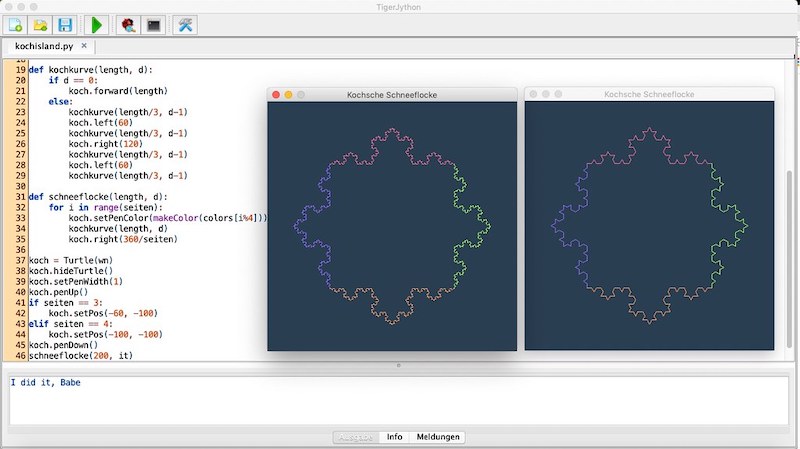
Die Kochsche Schneeflocke mit TigerJython. Rechts mit einer Iterationstiefe von drei, links mit einer Iterationstiefe von vier.

Man kann die Kurve anschaulich mittels eines iterativen Prozesses konstruieren Zu Beginn besteht die Kurve aus einem einzigen Streckenstück. Die Iteration besteht nun darin, daß dieser Streckenabschnitt durch einen anderen, aus vier gleich langen Strecken bestehenden Streckenabschnitt ersetzt wird, der wie folgt aufgebaut ist: Strecke – 60° Winkel – Strecke – 120° Winkel (in der Gegenrichtung) – Strecke – 60° Winkel – Strecke. Jeder der vier neuen Streckenabschnitte hat $1/3$ der Länge des ursprünglichen Streckenabschnitts. Im nächsten Schritt wird jeder der vier Streckenabschnitte durch einen Streckenabschnitt der oberen Art ersetzt. Diese Iteration wird nun beliebig oft wiederholt, wobei die Dreiecke stets zur selben Seite der Kurve hin zu errichten sind. Auf diese Weise ergibt sich eine Folge von Streckenzügen, die gegen die Koch-Kurve strebt. Im Grenzfall (nach unendlich vielen Iterationen) ist die Kochkurve unendlich lang, da der Streckenzug bei jeder Iteration um den Faktor $4/3$ länger wird.

Vergleicht man den Tiger-Jython-Quellcode mit dem Quellcode, den ich für (C) Pythons Schildkröte verwendet hatte, erkennt man, daß nur minimale Änderungen notwendig waren:

from gturtle import *

# Konstanten-Deklaration
WIDTH = 400
HEIGHT = 400

# Farben
colors = [(150, 100, 255), (255, 100, 150), (150, 255, 100), (255, 150, 100)]

seiten = 4      # Anzahl der Seiten der Schneeflocke,
                # entweder 3 oder 4
it = 3          # Iterationstiefe, entweder 3 oder 4

Options.setPlaygroundSize(WIDTH, HEIGHT)
wn = TurtleFrame()
wn.setTitle("Kochsche Schneeflocke")
wn.clear(makeColor("#2B3E50"))  # Hintergrundfarbe

def kochkurve(length, d):
    if d == 0:
        koch.forward(length)
    else:
        kochkurve(length/3, d-1)
        koch.left(60)
        kochkurve(length/3, d-1)
        koch.right(120)
        kochkurve(length/3, d-1)
        koch.left(60)
        kochkurve(length/3, d-1)

def schneeflocke(length, d):
    for i in range(seiten):
        koch.setPenColor(makeColor(colors[i%4]))
        kochkurve(length, d)
        koch.right(360/seiten)

koch = Turtle(wn)
koch.hideTurtle()
koch.setPenWidth(1)
koch.penUp()
if seiten == 3:
    koch.setPos(-60, -100)
elif seiten == 4:
    koch.setPos(-100, -100)
koch.penDown()
schneeflocke(200, it)
print("I did it, Babe")

Die Kochkurve wird spätestems seit Mandelbrot zur Simulation von Küstenlinien herangezogen. Und so ist die Kochsche Schneeflocke oder Insel auch ein Beispiel für ein Fläche mit einem endlichen Flächeninhalt aber einer unendlich langen Begrenzug.

Die Kochsche Insel oder Schneeflocke ist im Gegensatz zur Kochkurve nicht selbstähnlich.

Literatur

• Adrian Jablonski: Einführung in die fraktale Geometrie, korrigierte und überarbeitete Fassung vom 15. Juli 2017

• Benoit B. Mandelbrot; Die fraktale Geometrie der Natur, Basel (Birkhäuser) 1987, Seite 46-69

• Ian Stewart: Das Rätsel der Schneeflocke – Die Mathematik der Natur, München (Spektrum) 2007

(Kommentieren)