R entdecken: Die Lorenz-Gleichung in R

Als einer der ersten hatte 1961 Edward N. Lorenz, ein Meteorologe am Massachusetts Institute of Technology (MIT), erkannt, daß Iteration Chaos erzeugt. Er benutzte dort einen Computer, um ein einfaches nichtlineares Gleichungssystem zu lösen, das ein simples Modell der Luftströmungen in der Erdatmosphäre simulieren sollte. Dazu benutzte er ein System von sieben Differentialgleichungen, das Barry Saltzman im gleichen Jahr aus den Navier-Stokes-Gleichungen hergeleitet hatte. Für dieses System existierte keine analytische Lösung, also mußte es numerisch (d.h. wie damals und auch heute noch vielfach üblich in FORTRAN) gelöst werden. Lorenz hatte entdeckt, daß bei nichtperiodischen Lösungen der Gleichungen vier der sieben Variablen gegen Null strebten. Daher konnte er das System auf drei Gleichungen reduzieren:

$$\begin{align} \frac{dx}{dt} & = \gamma x + yz \\ \frac{dy}{dt} & = \sigma (y - z) \\ \frac{dz}{dt} & = -xy + \rho y - z \end{align} %$$

Dabei sind $\sigma = -10$, $\rho = 28$ und $\gamma = - \frac{8}{3}$. Die Parameter der Gleichung habe ich [Stew1993] entnommen.

Nach ersten Läufen gab Lorenz die Anfangswerte nicht mehr sechstellig (das war damals der FORTRAN-Standard), sondern nur noch dreistellig ein, da er der Meinung war, daß eine Abweichung von unter einem Promille keine Bedeutung habe.

Dabei entdeckte er, daß diese Lösung nur noch in den Anfangswerten mit der Lösung der sechsstelligen Eingabe übereinstimmte. Alle weiteren Werte liefen beträchtlich auseinander. Lorenz grundlegende Erkenntnis war, daß dieses Phänomen kein Computerfehler, sondern eine prinzipielle Eigenschaft nichtlinearer Gleichungssysteme ist. Schon die geringeste Änderung in den Anfangsbedingungen kann eine komplett andere Lösung hervorbringen. Diese Beobachtung ging später als »Schmetterlingseffekt« (»Der Schlag eines Schmetterlingsflügels in Brasilien kann einen Tornado über Texas hervorrufen.«) in die Geschichte der Chaostheorie ein.

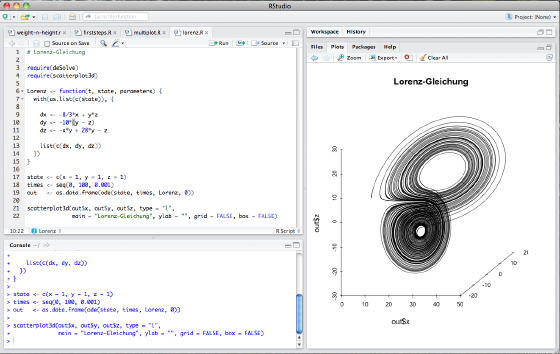
Angeregt durch [Soet2009], ein Buch, das ich gerade mit Vergnügen lese und [Chan2012], ein Buch, das ich hier schon mit Begeisterung besprochen hatte, wollte ich auch einmal ausprobieren, ob und wie sich R als Simulationsplattform eignet und habe die Lorenzgleichung in R nachprogrammiert. Wie man aus dem Screenshot erkennen kann, habe ich nicht die schnöde Konsole, sondern RStudio als Arbeitsumgebung gewählt. Noch haben sich mir nicht alle Vorzüge von RStudio erschlossen, doch alleine die komfortable Sessionverwaltung wie der einfache Graphik-Export haben mir gefallen.

Wie ich auf mehreren Workshops und Tagungen erfahren konnte, ist R bei Biologen und Ökologen sehr beliebt, da es nicht nur komfortabel statistische Auswertungen erledigt, sondern auch Pakete zur numerischen Lösung von Differentialgleichungen besitzt. Solch ein Paket (deSolve) und auch eines zur dreidimensionalen Darstellung (scatterplot3d) müssen zuerst geladen werden:

require(deSolve)
require(scatterplot3d)

Beide Pakete gehören nicht zum Standard-Lieferumfang von R, müssen also gegebenenfalls nachinstalliert werden. Aber auch dabei hilft RStudio mit dem integrierten Paketmanager.

Um eine Differentialgleichung zu lösen, muß sie erst einmal als Funktion definiert werden:

Lorenz <- function(t, state, parameters) {
  with(as.list(c(state)), {

    dx <- -8/3*x + y*z
    dy <- -10*(y - z)
    dz <- -x*y + 28*y - z

    list(c(dx, dy, dz))
  })
}

Man kann leicht obige Gleichungen und ihre Parameter wiedererkennen. Als nächstes werden die Anfangsbedingungen (state) und die Anzahl der Schritte und die Schrittweite (times) definiert:

state <- c(x = 1, y = 1, z = 1)
times <- seq(0, 100, 0.001)

Dann wird die Funktion ode aufgerufen, um die Gleichung zu lösen und die gefundenen Lösungen als data.frame abzuspeichern.

out   <- as.data.frame(ode(state, times, Lorenz, 0))

Dies dauerte auf meinem MacBook Pro einige Sekunden, etwas Geduld ist daher angebracht.

Zu guter Letzt wird mit scatterplot3d das Ergebnis gezeichnet:

scatterplot3d(out$x, out$y, out$z, type = "l",
              main = "Lorenz-Gleichung", ylab = "", grid = FALSE, box = FALSE)

Der Plot kann dann in hoher Qualität und Auflösung mit Hilfe der Export-Funktion von RStudio im Format Eurer Wahl abgespeichert werden.

Links

• Der Lorenz Attractor auf Wolfram MathWorld

Literatur

• [Chan2012] Sau Sheong Chang: Exploring Everyday Things with R and Ruby, Sebastopol (O’Reilly) 2012
• [Herm1994] Dieter Hermann: Algorithmen für Chaos und Fraktale, Bonn (Addison-Wesley) 1994, S. 80ff.
• [Pief1991] Frank Piefke: Simulationen mit dem Personalcomputer, Heidelberg (Hüthig) 1991
• [Soet2009] Karline Soetaert, Peter M.J. Hermann: A Practical Guide to Ecological Modelling: Using R as a Simulation Platform, o.O. (Springer Netherlands) 2009
• [Stew1993] Ian Stewart: Spielt Gott Roulette?, Frankfurt (Insel TB) 1993

---

---