Die Julia-Menge in Processing.py

Die Julia-Menge wurde 1918 von den beiden französischen Mathematikern Gaston Maurice Julia (nachdem sie benannt wurde) und Pierre Fatou (dessen Zugang heute die meisten Lehrbücher folgen) unabhängig voneinander beschrieben. Sie steht im engen Zusammenhang zur zuletzt beschriebenen Mandelbrot-Menge. Während die Mandelbrot-Menge, die Menge aller komplexen Zahlen c ist, die der iterierten Gleichung

$$\begin{align} z_{0} & = 0\\\\ z_{n+1} & = z_{n}^{2}+c\\\\ \end{align} %$$

folgen, ist bei der Julia-Menge c konstant:

$$\begin{align} z_{n}^{2}+c\\\\ \end{align}$$

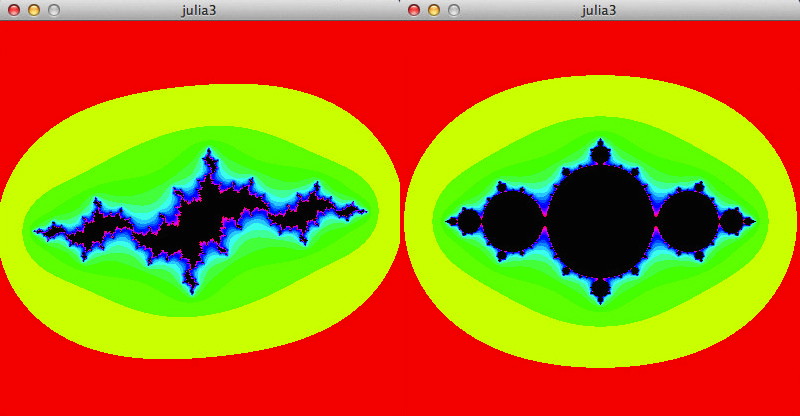
Die Mandelbrot-Menge ist also eine Beschreibungsmenge aller Julia-Mengen. Jedem Punkt c der komplexen Zahlenebene entspricht eine Julia-Menge. Eigenschaften der Julia-Menge lassen sich an der Lage von c relativ zur Mandelbrot-Menge beurteilen: Wenn der Punkt c Element der Mandelbrot-Menge ist, dann ist die Julia-Menge zusammenhängend. Andernfalls ist sie eine Cantormenge unzusammenhängender Punkte. Ist der Imaginärteil c_i = 0, dann ist die Julia-Menge symmetrisch (vlg. Abbildung links oben), ansonsten kann sie alle möglichen Formen annehmen.

Julia-Menge interaktiv

Ich habe die obigen Bilder mit diesem Programm erzeugt, daß den Parameter c in Abhängigkeit von der Mausposition setzt:

left   = -2.0
right  = 2.0
bottom = 2.0
top    = -2.0
maxlimit = 3.0
maxiter = 25

def setup():
    size(400, 400)
    background("#555ddd")
    colorMode(HSB, 1)

def draw():
    cr = map(mouseX, 0, width, left, right)
    ci = 0
    # ci = map(mouseY, 0, height, top, bottom)
    c = complex(cr, ci)
    for x in range(width):
        zr = left + x*(right - left)/width
        for y in range(height):
            zi = bottom + y*(top - bottom)/height
            z = complex(zr, zi)
            i = 0
            for i in range(maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter-1):
                    set(x, y, color(0))
                else:
                    set(x, y, color(sqrt(float(i)/maxiter), 100, 100))
    println("cr = " + str(cr))
    println("ci = " + str(ci))

Kommentiert man die Zeile ci = 0 aus und aktiviert stattdessen die auskommentierte Zeile darunter, erhält man (theoretisch) alle Julia-Mengen, sonst erzeugt das Programm nur die symmetrischen. Richtig flüssig ist die Animation allerdings nicht, Processing.py gerät – zumindest auf meinem betagten MacBook Pro – schon ganz schön ins Stottern.

Julia-Menge animiert

Das gilt auch für das zweite Programm, das die Parameter der Julia-Menge anhand zweier Sinus- (wahlweise auch Cosinus-) Funktionen periodisch durchläuft:

left   = -2.0
right  = 2.0
bottom = 2.0
top    = -2.0
maxlimit = 3.0
maxiter = 25

def setup():
    size(400, 400)
    background("#555ddd")
    colorMode(HSB, 1)

def draw():
    # cr = 0
    cr = 2*sin(frameCount)
    ci = 0
    # ci = 2*cos(frameCount)
    c = complex(cr, ci)
    for x in range(width):
        zr = left + x*(right - left)/width
        for y in range(height):
            zi = bottom + y*(top - bottom)/height
            z = complex(zr, zi)
            i = 0
            for i in range(maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter-1):
                    set(x, y, color(0))
                else:
                    set(x, y, color(sqrt(float(i)/maxiter), 100, 100))
    println("cr = " + str(cr))
    println("ci = " + str(ci))

Auch hier kommt das Programm ganz schön ins Schwitzen. Das läßt allerdings dem Betrachter Zeit, die Schönheit der Julia-Menge zu bewundern.

Caveat

Auch dieses Processing.py-Tutorial habe ich, wie alle anderen auch, auf meine eigens dafür eingerichtete Site »Processing.py lernen« hochgeladen. Änderungen, Korrekturen und Ergänzungen wird es nur dort geben.

---

1 (Email-) Kommentar

---

„Während die Mandelbrot-Menge, die Menge aller komplexen Zahlen c ist, die der iterierten Gleichung […] folgen […]“
Nicht eher „Während die gefüllte Mandelbrot-Menge die Menge aller komplexen Zahlen c ist, für die die iterierte Gleichung […] nicht gegen Unendlich konvergiert“?
Allerdings dachte ich immer, die Mandelbrotmenge sei eigentlich die Menge komplexer Zahlen, die unter Iteration der bekannten komplexwertigen Funktion auf sich selbst abgebildet wird.

– Moss (Kommentieren) (#)

---

(Kommentieren)