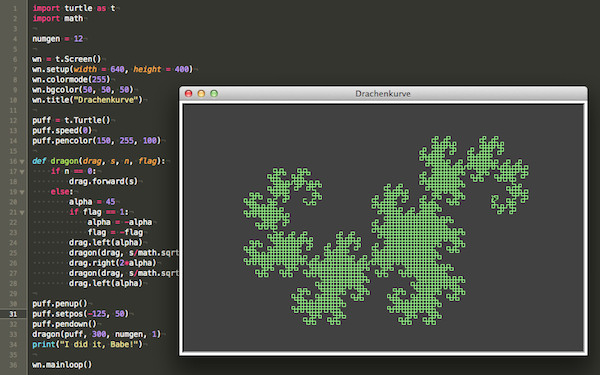
Turtle-Graphik (5): Die Drachenkurve

Die Drachenkurve ist ein fraktales Objekt, das ähnlich wie die Koch-Kurve und die Hilbert-Kurve durch Ersetzung erzeugt wird. Sie wurde von den amerikanischen Mathematikern Harter und Heightway erfunden und durch eine Artikelserie im Scientific American vom März 1967 populär.

Eine anschauliche Methode, die Drachenkurve zu erzeugen, ist folgende:

• Man nehme einen Papierstreifen und falte ihn in der Mitte, so daß sich seine Länge halbiert.
• Dies wiederhole man beliebig oft, dabei ist darauf zu achten, daß jedes mal in dieselbe Richtung gefaltet wird.
• Zum Schluß falte man das Papier auseinander und ordne es so an, daß die Innenwinkel der Falze immer 90° betragen.

Die Drachenkurve ist strikt selbstähnlich und im Grenzfall flächenfüllend, das heißt, die fraktale Dimension ist 2.

Quellcode

Auch für die Programmierung der Drachenkurve bietet sich das Turtle-Modul von Python geradezu an:

import turtle as t
import math

numgen = 12

wn = t.Screen()
wn.setup(width = 640, height = 400)
wn.colormode(255)
wn.bgcolor(50, 50, 50)
wn.title("Drachenkurve")

puff = t.Turtle()
puff.speed(0)
puff.pencolor(150, 255, 100)

def dragon(drag, s, n, flag):
    if n == 0:
        drag.forward(s)
    else:
        alpha = 45
        if flag == 1:
            alpha = -alpha
            flag = -flag
        drag.left(alpha)
        dragon(drag, s/math.sqrt(2), n-1, -flag)
        drag.right(2*alpha)
        dragon(drag, s/math.sqrt(2), n-1, flag)
        drag.left(alpha)

puff.penup()
puff.setpos(-125, 50)
puff.pendown()
dragon(puff, 300, numgen, 1)
print("I did it, Babe!")

wn.mainloop()

Auch wenn ich schon mit t.speed(0) die höchstmögliche Geschwindigkeit eingestellt habe, dauert es eine Zeit, bis die Drachenkurve fertig gezeichnet ist. Man kann dafür aber während des Programmablaufes sehr schön die Entstehung der Kurve beobachten.

Literatur

• Reimund Albers: Papierfalten, Dissertation zur Erlangung des Grades eines Doktors der Naturwissenschaften, Bremen (UB Bremen) 2006
• Eine weitere Seite von Reimund Albers zum Thema Papierfalten und Drachenkurve mit weiterführenden Links
• Jürgen Giese: Papierfalten, letzte Änderung am 12. März 2003
• Martin Große-Schulte: Eine neue Kodierung für die Papierfaltungsfolge, Bremen (UB) 2010
• Dietmar Herrmann: Algorithmen für Chaos und Fraktale, Bonn (Addison-Wesley) 1994, Seiten 163-166

• Courbe du Dragon
• Drachenkurve in der Wikipedia

(Kommentieren)