Spaß mit Mathematik: Spirographen mit Processing.py

Ein Spirograph ist ein mathematisches Spielzeug, mit dem man geometrische Muster oder mathematische Kurven zeichnen kann. In seiner einfachsten Form besteht er aus einem äußeren Zahnradkreis und einer inneren Zahnradscheibe mit mehreren Löchern (die meisten Spirographen haben mehrere, verschieden große innere (manchmal auch äußere) Zahnradscheiben, die dadurch noch mehr unterschiedliche Muster erzeugen können). Steckt man einen Stift in eines der Löcher und bewegt die Zahnradscheibe am äußeren Zahnradkranz, entstehen verschiedene, geometrische Figuren, sogenannte Hypozykloiden und Epizykloiden.

Das Spielzeug wurde 1965 von Denys Fisher auf der Nürnberger Spielwarenmesse vorgestellt. Doch es gab schon früher mindestens zwei Erfinder, die sich Spiralenzeichner patentieren ließen: Bruno Abdank-Abakanowicz im Jahre 1885, sowie Ernst Barthel im Jahre 1933.

Ich möchte mit Euch so einen Spirographen in Processing.py, dem Python-Mode von Processing entwickeln. Dabei folge ich wieder einer Idee aus dem schon mehrfach erwähnten Buch »Math Adventures with Python« von Peter Farrell, die ich aufgegriffen und weiterentwickelt habe.

In meiner Version zeichne ich zuerst einen äußeren und dann einen inneren Kreis. Der innere Kreis erhält einen malenden Punkt (im Programm rot). Damit der innere Kreis in dem äußeren rotiert, lasse ich ihn (in Polarkoordinaten) in Abhängigkeit von der Zeitvariable t im inneren Kreis umherdrehen:

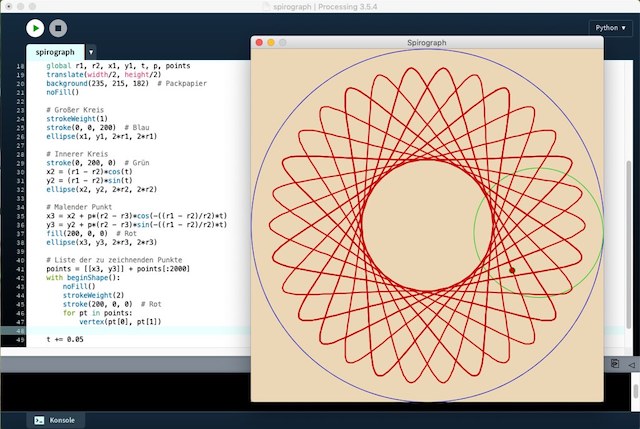
r1 = 300.0  # Radius großer Kreis (width/2)
r2 = 110.0  # Radius innerer Kreis
r3 = 5.0    # Radius malender »Punkt«

# Großer Kreis
x1 = 0
y1 = 0
t = 0
p = 0.75
points = []

def setup():
    size(600, 600)
    this.surface.setTitle("Spirograph")

def draw():
    global r1, r2, x1, y1, t, p, points
    translate(width/2, height/2)
    background(235, 215, 182)  # Packpapier
    noFill()
    
    # Großer Kreis
    strokeWeight(1)
    stroke(0, 0, 200)  # Blau
    ellipse(x1, y1, 2*r1, 2*r1)
    
    # Innerer Kreis
    stroke(0, 200, 0)  # Grün
    x2 = (r1 - r2)*cos(t)
    y2 = (r1 - r2)*sin(t)
    ellipse(x2, y2, 2*r2, 2*r2)
    
    # Malender Punkt
    x3 = x2 + p*(r2 - r3)*cos(-((r1 - r2)/r2)*t)
    y3 = y2 + p*(r2 - r3)*sin(-((r1 - r2)/r2)*t)
    fill(200, 0, 0)  # Rot
    ellipse(x3, y3, 2*r3, 2*r3)
    
    t += 0.05

Damit dies funktioniert, müssen wir noch die Konstante p global deklarieren (p steht für Proportion). Die Werte für p und r2 bestimmen die Form der Zykloide, die der Spirograph zeichnet. Um sie zu zeichnen, wird die Lieste points mit Werten gefüllt. Dafür muß vor der letzten Zeile des Sketches noch folgendes Codeschnipsel eingefügt werden:

    # Liste der zu zeichnenden Punkte
    points = [[x3, y3]] + points[:2000]
    with beginShape():
        noFill()
        strokeWeight(2)
        stroke(200, 0, 0)  # Rot
        for pt in points:
            vertex(pt[0], pt[1])

Wenn Ihr den Sketch nun laufen laßt, entsteht die Zeichnung aus dem Screenshot oben (r2 = 110 und p = 0.75). Ihr könnt diese beiden Werte ändern, um mehr oder weniger schöne Kurven zu erhalten.

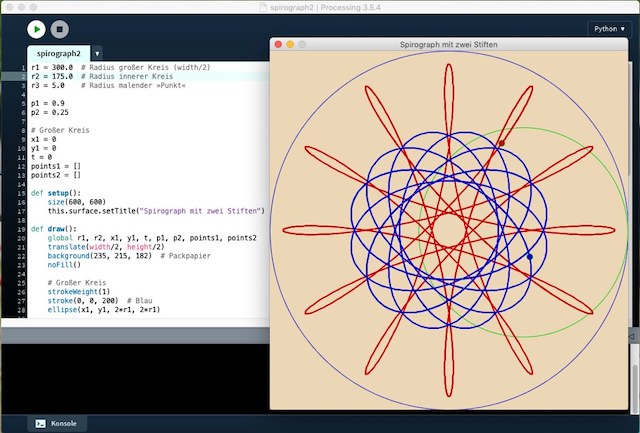
Doch es geht noch weiter. Was, wenn die innere Scheibe ein zweites Loch erhält und dieses mit einem andersfarbigen Stift gefüllt wird? Um dies durchzuspielen, habe ich r2 = 175 gesetzt (um mehr Platz im inneren Kreis zu haben) und zwei p eingeführt: p1 = 0.9 und p2 = 0.25. Natürlich brauchte ich dann auch noch zwei unabhängige Listen ( points1 und points2). Mit diesen wenigen Änderungen erhielt ich folgende zwei Kurven, die einen Spirographen mit zwei Stiften simulieren:

Wie immer zum Schluß der vollständige Sketch. Wenn man einmal von den vielen Deklarationen im Kopf absieht, ist er immer noch ziemlich kurz geraten:

r1 = 300.0  # Radius großer Kreis (width/2)
r2 = 175.0  # Radius innerer Kreis
r3 = 5.0    # Radius malender »Punkt«

p1 = 0.9
p2 = 0.25

# Großer Kreis
x1 = 0
y1 = 0
t = 0
points1 = []
points2 = []

def setup():
    size(600, 600)
    this.surface.setTitle("Spirograph mit zwei Stiften")

def draw():
    global r1, r2, x1, y1, t, p1, p2, points1, points2
    translate(width/2, height/2)
    background(235, 215, 182)  # Packpapier
    noFill()
    
    # Großer Kreis
    strokeWeight(1)
    stroke(0, 0, 200)  # Blau
    ellipse(x1, y1, 2*r1, 2*r1)
    
    # Innerer Kreis
    stroke(0, 200, 0)  # Grün
    x2 = (r1 - r2)*cos(t)
    y2 = (r1 - r2)*sin(t)
    ellipse(x2, y2, 2*r2, 2*r2)
    
    # Malender Punkt 1
    x3 = x2 + p1*(r2 - r3)*cos(-((r1 - r2)/r2)*t)
    y3 = y2 + p1*(r2 - r3)*sin(-((r1 - r2)/r2)*t)
    fill(200, 0, 0)  # Rot
    ellipse(x3, y3, 2*r3, 2*r3)
    
    # Malender Punkt 2
    x4 = x2 - p2*(r2 - r3)*cos(-((r1 - r2)/r2)*t)
    y4 = y2 - p2*(r2 - r3)*sin(-((r1 - r2)/r2)*t)
    fill(0, 0, 200)  # Blau
    ellipse(x4, y4, 2*r3, 2*r3)

    # Liste der zu zeichnenden Punkte
    points1 = [[x3, y3]] + points1[:2000]
    points2 = [[x4, y4]] + points2[:2000]
    noFill()
    strokeWeight(2)
    with beginShape():
        for pt1 in points1:
            stroke(200, 0, 0)  # Rot
            vertex(pt1[0], pt1[1])
    with beginShape():
        for pt2 in points2:
            stroke(0, 0, 200)  # Blau
            vertex(pt2[0], pt2[1])

    t += 0.05

Ich bin auf den Geschmack gekommen und da man wegen Corona sowieso Abstand zu anderen Menschen halten soll, werde ich die nächste Zeit mehr in meiner Kemenate meinem Arbeitszimmer verbringen und mich auf weitere mathematische Abenteuerreisen mit dem Computer begeben. Schaun wir mal, was dabei herauskommt.

(Kommentieren)