Theoretische Biologie: Die Lotka-Volterra-Gleichungen in Maxima

Die Lotka-Volterra-Gleichungen (auch als Räuber-Beute-Gleichungen bekannt) sind ein System aus zwei nicht-linearen, gekoppelten Differentialgleichungen erster Ordnung. Sie beschreiben die Wechselwirkung von Räuber- und Beutepopulationen. Unter Räuber und Beute sind dabei zwei Klassen von Lebewesen gemeint, wobei die eine sich von der anderen ernährt. Aufgestellt wurden die Gleichungen 1925 von Alfred J. Lotka und, unabhängig davon, 1926 von Vito Volterra. Sie sind eine wichtige Grundlage der Theoretischen Biologie, und darin insbesondere der Populationsdynamik. Bei den Räubern und der Beute muß es sich nicht unbedingt nur um Tiere oder einzelne Arten handeln, neben der Theoretische Biologie finden in der medizinischen Epidemologie Modelle vom Lotka-Volterra-Typ zur Beschreibung der Ausbreitungsprozesse von Krankheiten Verwendung, zum Beispiel im SI-Modell, SIR-Modell und SIS-Modell.

Da ich das SIR-Modell ja schon in Maxima vorgestellt hatte, lag es natürlich nahe, daß ich es auch einmal mit den Lotka-Volterra-Gleichungen versuchen wollte. Die beiden Gleichungen lauten

wobei

• $N_1 = N_1(t)$ die Anzahl der Beutetiere und
• $N_2 = N_2(t)$ die Anzahl der Räuber ist. Die Konstanten bedeuten:
• $\epsilon_1 > 0$ ist die Reproduktionsrate der Beute ohne Störung und bei ausreichendem Nahrungsangebot.
• $\gamma_1 > 0$ ist die Freßrate der Räuber pro Beutelebewesen = Sterberate der Beute pro Räuber.
• $\epsilon_2 > 0$ ist die Sterberate der Räuber, wenn keine Beute vorhanden ist.
• $\gamma_2 > 0$ ist die Reproduktionsrate der Räuber pro Beutelebewesen.

In Maxima habe ich erst einmal das Gleichungssystem eingegeben:

(%i2)   g1: 0.5*x - 0.0333*x*y;
        g2: -1.0*y + 0.01*x*y;
        
(g1)    0.5*x\-0.0333*x*y
(g2)    0.01*x*y\-1.0*y

(%i4)   B0: 100;
        R0: 45;
        
(B0)    100
(R0)    45

(%i5)   tMax: 50;

(tMax)  50

Dabei habe ich $\epsilon_1 = 0.5$, $\gamma_1 = 0.333$, $\epsilon_2 = 1.0$ und $\gamma_2 = 0.01$ gesetzt. Anfangswerte der Beutetiere sind 100 und der Räuber 45. Der Zeitraum geht über eine Zeit von 50 (Tagen). Die Werte habe ich aus dem Buch von Frank Piefke¹ entnommen.

Dann habe ich das Runge-Kutta-Verfahren zur Lösung der Differentialgleichung bemüht und anschließend die verschachtelte Listen wieder in einzelne Listen aufgesplittet:

(%i6)   result: rk([g1, g2], [x, y], [B0, R0], [t, 0, tMax, 0.01])$

(%i9)   lit: map(first, result)$
        liB: map(second, result)$
        liR: map(third, result)$

Zu guter Letzt habe ich dann noch ein paar Default-Plot-Optionen gesetzt:

(%i10)  set_draw_defaults(point_type=0, point_size=0, points_joined=true,
        color=red, grid=true);
(%o10)  [point_type=0,point_size=0,points_joined=true,color=red,grid=true]

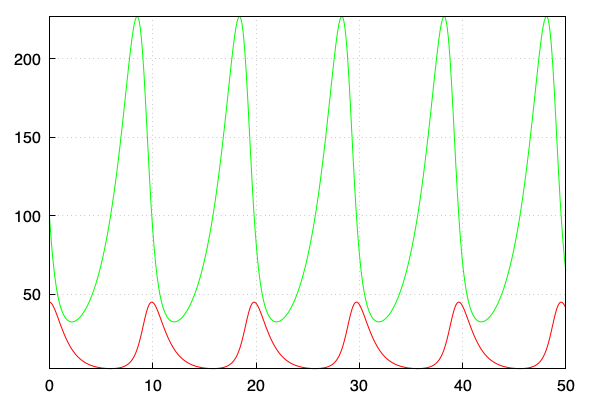
Der Befehl

(%i11)        wxdraw2d(points(lit, liR), color=green, points(lit, liB))$

plottete das Zeitdiagramm. Grün sind die Beutetiere eingezeichnet, rot sind die Räuber.

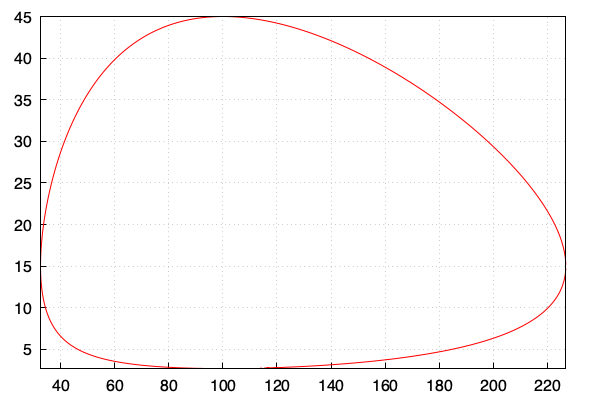
Interessant ist auch das Phasendiagramm, das die Anzahl der Beutetiere (x-Achse) über die Anzahl der Räuber (y-Achse) zeigt und mit untenstehendem Befehl erzeugt wurde:

(%i12)        wxdraw2d(points(liB, liR));

Man kann daran sehr gut die Periodizität des Systems erkennen.

Das war es dann für heute. Schaun wir mal, was für mathematische Spielereien ich beim nächsten Mal ausgrabe. Still digging!

(Kommentieren)