Conways Game of Life in Python mit der Matplotlib animiert

Conway’s Game of Life (GoL) ist ein vom Mathematiker John Horton Conway 1970 entworfenes Spiel, basierend auf einem zweidimensionalen zellulären Automaten. Es ist eine einfache und bis heute populäre Umsetzung der Automaten-Theorie von Stanisław Marcin Ulam.

Es fasziniert vor allem, weil die Spielregeln recht einfach gehalten sind: Das Spielfeld ist in Zeilen und Spalten unterteilt und im Idealfall unendlich groß. Jedes Gitterquadrat ist ein zellulärer Automat (Zelle), der einen von zwei Zuständen einnehmen kann, welche oft als lebendig und tot bezeichnet werden. Zunächst wird eine Anfangsgeneration von lebenden Zellen auf dem Spielfeld platziert. Jede lebende oder tote Zelle hat auf diesem Spielfeld genau acht Nachbarzellen, die berücksichtigt werden (Moore-Nachbarschaft). Die nächste Generation ergibt sich durch die Befolgung einfacher Regeln:

1. Eine tote Zelle mit genau drei lebenden Nachbarn wird in der Folgegeneration neu geboren.
2. Lebende Zellen mit weniger als zwei lebenden Nachbarn sterben in der Folgegeneration an Einsamkeit.
3. Eine lebende Zelle mit zwei oder drei lebenden Nachbarn bleibt in der Folgegeneration am Leben.
4. Lebende Zellen mit mehr als drei lebenden Nachbarn sterben in der Folgegeneration an Überbevölkerung.

Aus diesen vier einfachen Regeln entstehen unglaublich komplexe Muster. Einige bleiben unverändert, andere oszillieren und wieder andere wachsen oder vergehen. Manche Strukturen, sogenannte Gleiter, bewegen sich auf dem Spielfeld fort. Sogar logische Funktionen wie UND und ODER lassen sich durch bestimmte Anfangsmuster simulieren.

Da ich nun weiß, daß nun auch auf meinem Mac Animationen in Python mit der Matplotlib möglich sind, habe ich das Buch »Python Playground« von Mahesh Venkitachalam mal wieder hervorgekramt. Denn dort ist eine Version Spiels implementiert, die die Matplotlib nutzt. Durch dieses Programm wurde ich sogar erstmals auf die Animationsmöglichkeiten der Matplotlib aufmerksam und war damals sehr enttäuscht, daß sie auf dem Mac nicht funktionierte.

Mein Programm folgt weitestgehend dem Programm aus »Python Playground«, lediglich ein paar mir überflüssig erscheinende Spielereien (so zum Beispiel die Aufrufe von der Kommandozeile mit dem Argumentenparser) habe ich weggelassen und an einigen Stellen den Code optimiert. So ist bei mit ON = 1 und OFF = 0, statt 0 und 255, denn das ersparte mir eine Division durch 255. Außerdem habe ich als Colormap Viridis ausgewählt. Das ist – glaube ich – mittlerweile auch die Defaulteinstellung von FuncAnimation, aber Mahesh Venkitachalam hatte in seiner Version darauf vertraut, daß die Defaulteinstellung Hell- und Dunkelgrau hervorbringt, aber das hat sich zwischenzeitlich geändert. Und so habe ich explizit eine colormap-Variable angelegt, die Ihr mit der Farbpalette Eurer Wahl (sofern sie von Matplotlib unterstützt wird) belegen könnt.

Die gesamte Berechnung der Umgebung und Neubelegung der Zellen findet in der update()-Funktion statt. Da alle Zellen auf einmal überprüft werden müssen, kann die Änderung nicht im Spielfeld erfolgen, sondern es muß erst eine Kopie angelegt werden und erst, nachdem alle neuen Zustände in der Kopie eingetragen sind, wird diese für den nächsten Durchlauf wieder zum Original.

Da eine unendlich große Welt irgendwann den Speicherbedarf jedes Rechners sprengen würde, habe ich oben und unten, sowie rechts und links miteinander verklebt, so daß eine toroidiale Welt entsteht, also eine Welt in der Form eines Autoreifens.¹ Das ist eine vielfach genutzte Praxis, jedoch gibt es auch andere Möglichkeiten, die Unendlichkeit auf einem Rechner zu simulieren, zum Beispiel können alle Zellen außerhalb des Bildschirms grundsätzlich für tot oder OFF erklärt werden.

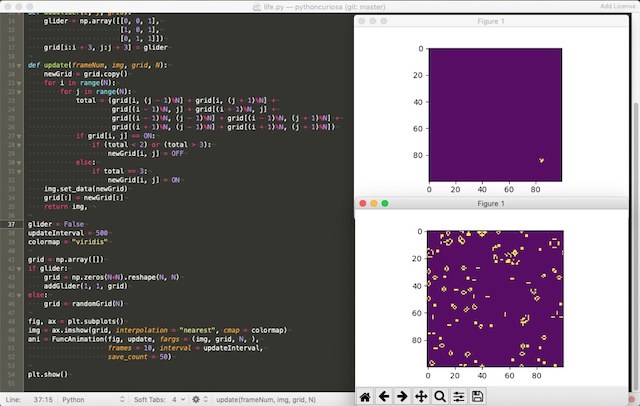
Obiger Screenshot zeigt das Programm in zwei verschiedenen Durchläufen. Im oberen Plot zieht ein einsamer Gleiter seine Bahn, während im unteren Plot eine zufällig generierte Zellkultur einem Endzustand zustrebt.

Nun aber das vollständige Script für alle, die das nachprogrammieren wollen:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation

N = 100
ON  = 1
OFF = 0
vals = [ON, OFF]

def randomGrid(N):
    return np.random.choice(vals, N*N, p = [0.2, 0.8]).reshape(N, N)

def addGlider(i, j, grid):
    glider = np.array([[0, 0, 1],
                       [1, 0, 1],
                       [0, 1, 1]])
    grid[i:i + 3, j:j + 3] = glider

def update(frameNum, img, grid, N):
    newGrid = grid.copy()
    for i in range(N):
        for j in range(N):
            total = (grid[i, (j - 1)%N] + grid[i, (j + 1)%N] +
                     grid[(i - 1)%N, j] + grid[(i + 1)%N, j] +
                     grid[(i - 1)%N, (j - 1)%N] + grid[(i - 1)%N, (j + 1)%N] +
                     grid[(i + 1)%N, (j - 1)%N] + grid[(i + 1)%N, (j + 1)%N])
            if grid[i, j] == ON:
                if (total < 2) or (total > 3):
                    newGrid[i, j] = OFF
            else:
                if total == 3:
                    newGrid[i, j] = ON
    img.set_data(newGrid)
    grid[:] = newGrid[:]
    return img, 

glider = False
updateInterval = 50
colormap = "viridis"

grid = np.array([])
if glider:
    grid = np.zeros(N*N).reshape(N, N)
    addGlider(1, 1, grid)
else:
    grid = randomGrid(N)

fig, ax = plt.subplots()
img = ax.imshow(grid, interpolation = "nearest", cmap = colormap)
ani = FuncAnimation(fig, update, fargs = (img, grid, N, ),
                    frames = 10, interval = updateInterval,
                    save_count = 50)

plt.show()

Wenn die Zeile glider = False durch glider = True ersetzt wird, erhaltet Ihr den Gleiter, ansonsten wird zufällig eine Anfangsstruktur erzeugt.

Es gibt natürlich noch viele weitere Strukturen in Life, die sich zu erkunden lohnen. Berühmt ist die Gleiterkanone, die ständig neue Gleiter in Spielfeld schickt, oder das f-Pentomino, das eine sagenhafte Lebenszeit von 1.102 Generationen besitzt, bevor es eine oszillierende Struktur bildet – aber nicht ohne vorher noch einige Gleiter in die Unendlichkeit zu schicken.

Ihr könnt eine Funktion schreiben, die diese Strukturen erzeugt, so wie ich es oben mit addGlider() gemacht habe, oder Ihr könnt die Strukturen auch von einer Datei einlesen lassen. Das ist bei größeren Strukturen, wie zum Beispiel einer Gleiterkanone, sicher sinnvoller.

Literatur

Conways Game of Life ist berühmt, die Literatur dazu ist riesig. Ich möchte ein paar ausgewählte Quellen vorstellen und kurz kommentieren:

• Gardner, Martin (October 1970). »Mathematical Games - The Fantastic Combinations of John Conway’s New Solitaire Game ‘Life’« (). Scientific American (223): pp. 120–123. Mit diesem Artikel, der auch übersetzt in der deutschen Schwesterzeitschrift Spektrum der Wissenschaft erschien (ich weiß aber nicht, wann), begann der Siegeszug von Game of Life.
• Martin Gerhard, Heike Schuster: »Das digitale Universum, Zelluläre Automaten als Modelle der Natur«, Braunschweig/Wiesbaden (Vieweg) 1995. Das umfangreichste Buch über zelluläre Automaten, das ich kenne. Es behandelt Life in einem ganzen Kapitel, stellt aber auch viele andere Modelle vor
• Karl Sigmund: »Spielpläne. Zufall, Chaos und die Strategien der Evolution«, München (Knaur) 1997. In diesem Buch findet Ihr fast alles, was es über Life und verwandte zelluläre Automaten zu wissen gibt. Und es ist dazu auch noch recht vergnüglich geschrieben.
• Daniel Scholz: »Pixelspiele, Modellieren und Simulieren mit zellulären Automaten«, Berlin/Heidelberg (Springer-Verlag) 2014. Das Lehrbuch ist das jüngste Buch zu zellulären Automaten in meiner Bibliothek. Es besitzt viele farbige Abbildungen und auf der Website zum Buch gibt es den Quellcode einiger Programme in JavaScript.

(Kommentieren)