Noch mehr Newton-Fraktale in Processing.py
Ich konnte es nicht lassen. Angefixt durch meinen eigenen Beitrag mußte ich am Wochenende noch ein wenig mit Processing.py spielen und weitere Newton-Fraktale programmieren:
Als erstes habe ich die Funktion f(z) = z6 - 1 plotten lassen. Die komplexe Ebene verlief dabei sowohl horizontal wie auch vertikal jeweils von -2 bis 2.
Bei diesen vielen Nullstellen blieb es nicht aus, daß mein Sketch eine komplexe Division durch 0 anmackerte. Das habe ich durch folgende Zeilen ausgeschlossen:
for i in range(maxIt): # Complex numerical derivative dz = (f(z + complex(h, h)) - f(z))/complex(h, h) if dz != 0: z0 = z - f(z)/dz # Newton iteration if abs(z0 - z) < eps: # Stop when close enough to any root break z = z0
Dann wurde ich etwas mutiger und ließ f(z) = z(z6 - 1) plotten. Die komplexe Ebene verlief wie im letzten Beispiel in beide Richtungen von -2 bis 2.
Dann wollte ich f(z) = sin(z) zeichnen lassen. Um die komplexe Sinusfunktion aufrufen zu können, mußte ich mit
import cmath
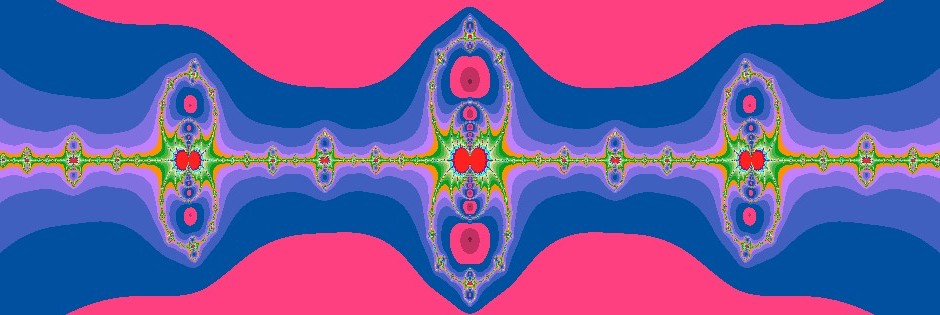
das Modul cmath mit ins Boot holen. Die komplexe Zahlenebene wurde in realer Richtung (horizontal) auf das Interval von 1,126 bis 2,0 begrenzt, während die imaginäre Ebene weiter von -2 bis auf 2 begrenzt war. Der obige Banner ist eine um 180 Grad gedrehte Version dieses Fraktals.
Und hier der Vollständigkeit halber noch der komplette Sketch:
import cmath imgx = 512 imgy = 512 # Drawing area # xa = 1.126 xa = -2.0 xb = 2.0 ya = -2.0 yb = 2.0 maxIt = 20 # max iterations allowed h = 1e-6 # stepsize for numerical derivative eps = 1e-3 # max error allowed def f(z): # return cmath.sin(z) # return z*z*z*z*z*z - 1.0 return z*(z*z*z*z*z*z - 1.0) def setup(): global img size(imgx, imgy) this.surface.setTitle("Newton Fractal (2)") img = createImage(width, height, RGB) noLoop() def draw(): global img loadPixels() img.loadPixels() for y in range(imgy): zy = y*(yb - ya)/(imgy - 1) + ya for x in range(imgx): zx = x*(xb - xa)/(imgx - 1) + xa z = complex(zx, zy) for i in range(maxIt): # Complex numerical derivative dz = (f(z + complex(h, h)) - f(z))/complex(h, h) if dz != 0: z0 = z - f(z)/dz # Newton iteration if abs(z0 - z) < eps: # Stop when close enough to any root break z = z0 loc = x + y*width # pixels[loc] = color(i%5*64, i%9*32, i%17*16) pixels[loc] = color(i%5*64, i%17*16, i%9*32) updatePixels() print("I did it, Babe!")
Durch Ein- beziehungsweise Auskommentieren der entsprechenden Zeilen könnt Ihr die einzelnen Versionen zeichnen lassen. Natürlich steht es Euch frei und ich fordere Euch auch ausdrücklich dazu auf, in f(z) mit eigenen komplexen Funktionen zu experimentieren. Wer weiß, vielleicht gibt es auch von mir noch ein paar weitere farbenfrohe Plots auf Basis der Newton-Iteration. Still digging!
Über …
Der Schockwellenreiter ist seit dem 24. April 2000 das Weblog digitale Kritzelheft von Jörg Kantel (Neuköllner, EDV-Leiter Rentner, Autor, Netzaktivist und Hundesportler — Reihenfolge rein zufällig). Hier steht, was mir gefällt. Wem es nicht gefällt, der braucht ja nicht mitzulesen. Wer aber mitliest, ist herzlich willkommen und eingeladen, mitzudiskutieren!
Alle eigenen Inhalte des Schockwellenreiters stehen unter einer Creative-Commons-Lizenz, jedoch können fremde Inhalte (speziell Videos, Photos und sonstige Bilder) unter einer anderen Lizenz stehen.
Der Besuch dieser Webseite wird aktuell von der Piwik Webanalyse erfaßt. Hier können Sie der Erfassung widersprechen.
Diese Seite verwendet keine Cookies. Warum auch? Was allerdings die iframes von Amazon, YouTube und Co. machen, entzieht sich meiner Kenntnis.
Werbung
Diese Spalte wurde absichtlich leergelassen!