Programmieren in der Pandemie: Der Metzler-Attraktor

Da ich durch die gestrige Beschäftigung mit dem erstem Band der zweibändigen Chaos-Bibel »Chaos – Bausteine der Ordnung« von Heinz-Otto Peitgen, Hartmut Jürgens und Dietmar Saupe angefixt worden bin, habe ich mich heute gleich wieder hingesetzt und in Processing.py einen seltsamen Attraktor, nämlich den Metzler-Attraktor, programmiert:

Ein seltsamer Attraktor ist – so schreibt es die Wikipedia – ein Attraktor, also ein Ort im Phasenraum, der den Endzustand eines dynamischen Prozesses darstellt, dessen fraktale Dimension nicht ganzzahlig ist. Es handelt sich damit um ein Fraktal, das nicht in geschlossener Form geometrisch beschrieben werden kann. Gelegentlich wird auch der Begriff chaotischer Attraktor bevorzugt, da die »Seltsamkeit« dieses Objekts sich mit den Mitteln der Chaostheorie erklären läßt. Der dynamische Prozess zeigt ein aperiodisches Verhalten.

Der Metzler-Attraktor wurde 1983 in dem Beitrag »Symmetry and Selfsimilarity with Coupled Logistic Maps« von W. Metzler, W. Beau, W. Frees und A. Überla in der »Z. f. Naturforsch. 42a« publiziert. Wie der Titel schon verrät, entsteht er aus einer gekoppelten, zweiparametrischen logistischen Gleichung:

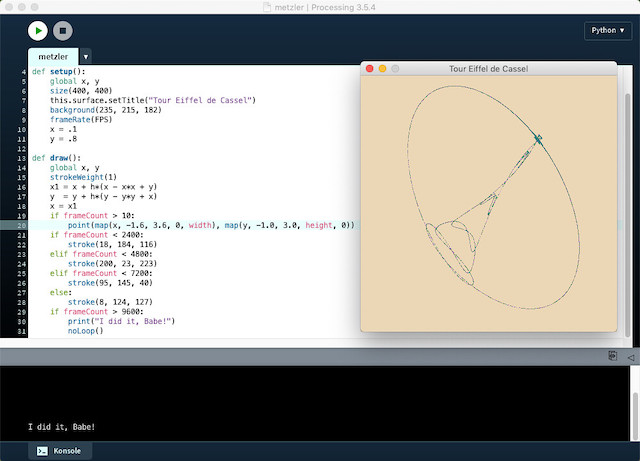
Ab $h = 0.648$ tritt Chaos auf. Für diesen Wert bildet sich das Intervall [1.3, 1.3] auf sich selbst ab. Da der dabei entstehende Attraktor Ähnlichkeiten mit dem Eiffelturm aufweist, wird er häufig auch Tour Eiffel de Cassel nach der Institutsstadt Kassel genannt.

Ich habe diesen Attraktor mit folgendem Processing.py-Skript erzeugt:

h = .684
FPS = 900

def setup():
    global x, y
    size(400, 400)
    this.surface.setTitle("Tour Eiffel de Cassel")
    background(235, 215, 182)
    frameRate(FPS)
    x = .1
    y = .8

def draw():
    global x, y
    strokeWeight(1)
    x1 = x + h*(x - x*x + y)
    y  = y + h*(y - y*y + x)
    x = x1
    if frameCount > 10:
        point(map(x, -1.6, 3.6, 0, width), map(y, -1.0, 3.0, height, 0))
    if frameCount < 2400:
        stroke(18, 184, 116)
    elif frameCount < 4800:
        stroke(200, 23, 223)
    elif frameCount < 7200:
        stroke(95, 145, 40)
    else:
        stroke(8, 124, 127)
    if frameCount > 9600:
        print("I did it, Babe!")
        noLoop()

Um den Attraktor sichtbar zu machen, habe ich ihn mit map(x, -1.6, 3.6, 0, width), map(y, -1.0, 3.0, height, 0) auf Fenstergröße skaliert. Und damit man nicht minutenlang warten muß, habe ich die frameRate auf 900 gesetzt. Das scheint mein kleines Rechnerchen gerade noch zu fressen, bei höheren Frameraten habe ich keine Gewschwindigkeitsverbesserung mehr festgestellt.

Die Gleichung habe ich 1:1 in den Sketch eingesetzt, der Rest ist Kosmetik. Viel Spaß damit.

Wer mehr über Chaostheorie und Fraktale wissen will, dem empfehle ich den Beitrag Fraktale Geomeotrie (, 62 Seiten) von der Seite Mathematik alpha.

(Kommentieren)