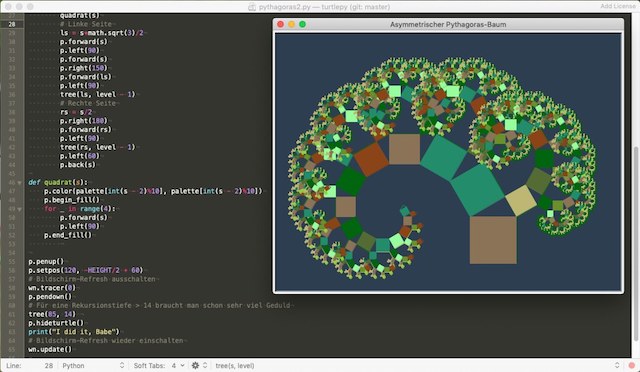
Ein asymmetrischer Pythagoras-Baum mit Python und der Turtle
Ich konnte es nicht lassen, ich mußte mal wieder mit (C-)Pythons Turtle-Modul spielen. Denn nur mit wenigen Änderungen im Quellcode des symmetrischen Pythagoras-Baumes, den ich vor ein paar Tagen implementiert hatte, läßt sich ein asymmetrischer Pythagoras-Baum zusammenbasteln:
Da in dieser Implementierung die rechte und die linke Seite des Baumes getrennt behandelt werden, macht es Sinn, die Rekursionstiefe von der Seitenlänge zu entkoppeln, denn sonst wartet man ewig, bis eine Abbildung des Baumes im Fenster erscheint. Auf meinem betagten MacBook Pro war die Wartezeit bei einer Rekursionstiefe von vierzehn (level = 14) gerade noch erträglich, für fünfzehn habe ich mich mit sehr viel Geduld gewappnet und sechzehn habe ich gar nicht erst in Angriff genommen.
Hier nun wie immer der Quellcode:
import turtle as t import math WIDTH = 640 HEIGHT = 480 palette = [(189, 183, 110), (34, 139, 105), (154, 205, 50), (139, 115, 85), (85, 107, 47), (139, 69, 19), (107, 142, 35), (139, 134, 78), (152, 251, 152), (0, 100, 0)] wn = t.Screen() wn.colormode(255) wn.bgcolor("#2b3e50") wn.setup(width = WIDTH, height = HEIGHT) wn.title("Asymmetrischer Pythagoras-Baum") p = t.Turtle() p.speed(0) p.color(0, 100, 0) p.setheading(90) def tree(s, level): if level < 1: return else: quadrat(s) # Linke Seite ls = s*math.sqrt(3)/2 p.forward(s) p.left(90) p.forward(s) p.right(150) p.forward(ls) p.left(90) tree(ls, level - 1) # Rechte Seite rs = s/2 p.right(180) p.forward(rs) p.left(90) tree(rs, level - 1) p.left(60) p.back(s) def quadrat(s): p.color(palette[int(s - 2)%10], palette[int(s - 2)%10]) p.begin_fill() for _ in range(4): p.forward(s) p.left(90) p.end_fill() p.penup() p.setpos(120, -HEIGHT/2 + 60) # Bildschirm-Refresh ausschalten wn.tracer(0) p.pendown() # Für eine Rekursionstiefe > 14 braucht man schon sehr viel Geduld tree(85, 14) p.hideturtle() print("I did it, Babe") # Bildschirm-Refresh wieder einschalten wn.update() wn.mainloop()
Ich habe die Farben in der Palette noch ein wenig verschoben, um auch hier ein ansprechbares Erscheinungsbild (siehe Screenshot) zu bekommen.
Ganz Mutige können ja mal wn.tracer(0) und wn.update() auskommentieren, um zu sehen, wie sich der Pythagoras-Baum aufbaut, aber dann sollte man die Rekursiontiefe nicht größer sieben wählen.
Über …
Der Schockwellenreiter ist seit dem 24. April 2000 das Weblog digitale Kritzelheft von Jörg Kantel (Neuköllner, EDV-Leiter Rentner, Autor, Netzaktivist und Hundesportler — Reihenfolge rein zufällig). Hier steht, was mir gefällt. Wem es nicht gefällt, der braucht ja nicht mitzulesen. Wer aber mitliest, ist herzlich willkommen und eingeladen, mitzudiskutieren!
Alle eigenen Inhalte des Schockwellenreiters stehen unter einer Creative-Commons-Lizenz, jedoch können fremde Inhalte (speziell Videos, Photos und sonstige Bilder) unter einer anderen Lizenz stehen.
Der Besuch dieser Webseite wird aktuell von der Piwik Webanalyse erfaßt. Hier können Sie der Erfassung widersprechen.
Diese Seite verwendet keine Cookies. Warum auch? Was allerdings die iframes von Amazon, YouTube und Co. machen, entzieht sich meiner Kenntnis.
Werbung
Diese Spalte wurde absichtlich leergelassen!