Processing.py, Python und Numba im Geschwindigkeitsvergleich

Angeregt durch meinem Beitrag am Dienstag »Python (und P5?) beschleunigen mit Numba« habe ich mich selber an einige Experimente mit der Mandelbrotmenge und der Frage, wie schnell ich sie in Python auf den Monitor bekomme, gewagt. Den Anfang macht ein Vergleich zwischen Processing.py und »normalem« Python und dann habe ich geschaut, wie Numba Python beschleunigt. Ich muß sagen, die Ergebnisse waren überwältigend.

P5 (Python) mußte aus diesen Test leider herausfallen. Weder konnte ich in endlicher Geschwindigkeit die Mandelbrotmenge mit P5 erzeugen, noch konnte ich P5 mit Numba verheiraten. Entweder sind doch noch einige Bugs in P5 vorhanden oder es gibt Kompatibilitätslücken zwischen Processing (Java) und P5. Doch starten wir mit Processing.py:

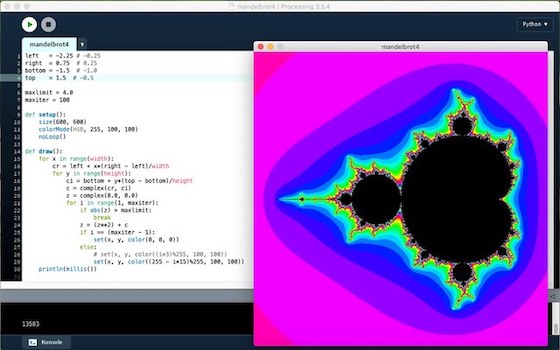
Als erstes habe ich Processing.py die vollständige Mandelbrotmenge mit einer einfachen Farbpalette und einer maximalen Anzahl von 100 Iterationen zeichnen lassen. Das Ergebnis materialisierte sich auf meinem betagten MacBook Pro mit einem 2.5 GHz Intel Core i5 Prozessor nach 13,5 Sekunden auf dem Monitor. Alle Berechnungen sind mit diesem Rechner erfolgt, die Ergebnisse daher vergleichbar.

Hier der vollständige Sketch:

left   = -2.25
right  = 0.75
bottom = -1.5
top    = 1.5

maxlimit = 4.0
maxiter = 100

def setup():
    size(600, 600)
    colorMode(HSB, 255, 100, 100)
    noLoop()

def draw():
    for x in range(width):
        cr = left + x*(right - left)/width
        for y in range(height):
            ci = bottom + y*(top - bottom)/height
            c = complex(cr, ci)
            z = complex(0.0, 0.0)
            for i in range(1, maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter - 1):
                    set(x, y, color(0, 0, 0))
                else:
                    # set(x, y, color((i*3)%255, 100, 100))
                    set(x, y, color((255 - i*15)%255, 100, 100))
    println(millis())

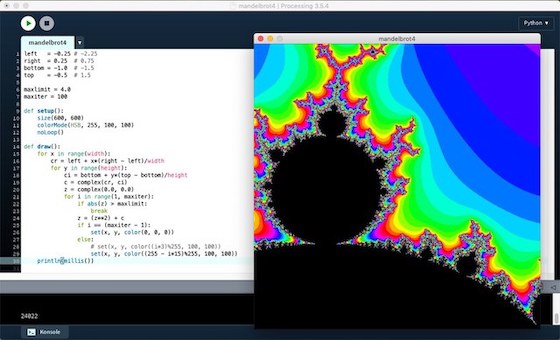
Für den nächsten Test habe ich einen Ausschnitt aus der Mandelbrotmenge gewählt (für alle Tests habe ich wegen der Vergleichbarkeit immer den gleichen Ausschnitt genommen):

left   = -0.25
right  = 0.25
bottom = -1.0
top    = -0.5

Ansonsten blieb der Sketch unverändert. Insbesondere die maximale Anzahl der Iterationen blieb bei 100. Dennoch brauchte der Sketch dieses Mal 24 Sekunden bis das Ergebnis auf dem Bildschirm erschien. Aber damit war zu rechnen, wegen des gewählten Ausschnittes mußte das Programm viel mehr Iterationen bis weit nach oben durchlaufen, um die Zugehörigkeit zur Mandelbrotmenge zu erkennen. Bei der vollständigen Mandelbrotmenge wird bei vielen Punkten schnell erkannt (die rot und pink gefärbten Bereiche), ob diese nicht zur Menge gehören, bei dem gewählten Ausschnitt mußte schon etwas mehr gerechnet werden.

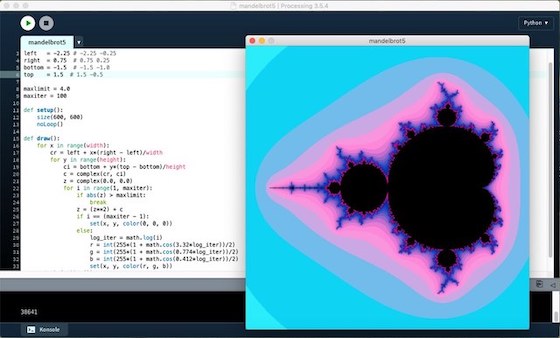
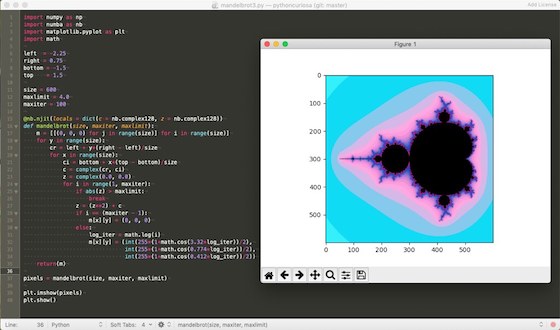
Dann habe ich mich bei den Experimenten von Ankit Mahato bedient, der – wohl um die Sache richtig rechenintensiv zu machen – die RGB-Werte der Farbpalette mit logarithmischer Darstellen und Cosinus-Berechnungen kalkulierte. Das Ergebnis sieht sogar richtig schick aus, aber selbst die komplette Mandelbrotmenge brauchte stolze 38,6 Sekunden, bevor sie in voller Schönheit auf dem Monitor erstrahlte.

Natürlich will ich Euch den Sketch nicht vorenthalten:

import math

left   = -2.25
right  = 0.75
bottom = -1.5
top    = 1.5

maxlimit = 4.0
maxiter = 100

def setup():
    size(600, 600)
    noLoop()

def draw():
    for x in range(width):
        cr = left + x*(right - left)/width
        for y in range(height):
            ci = bottom + y*(top - bottom)/height
            c = complex(cr, ci)
            z = complex(0.0, 0.0)
            for i in range(1, maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter - 1):
                    set(x, y, color(0, 0, 0))
                else:
                    log_iter = math.log(i)
                    r = int(255*(1 + math.cos(3.32*log_iter))/2)
                    g = int(255*(1 + math.cos(0.774*log_iter))/2)
                    b = int(255*(1 + math.cos(0.412*log_iter))/2)
                    set(x, y, color(r, g, b))
    println(millis())

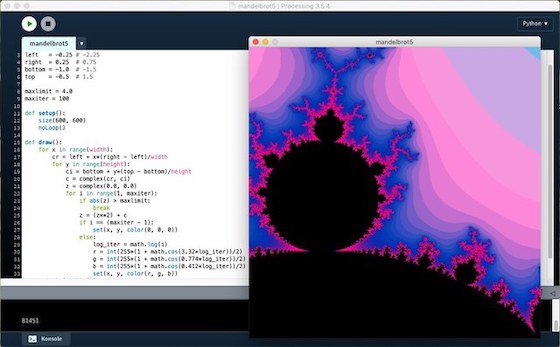
Der letzte Test mit Processing.py lief mit dem oben angezeigten Ausschnitt aus der Mandelbrotmenge mit der gleichen komplexen Farbpalette. Wie in all den anderen Experimenten, war auch hier die maximale Iterationstiefe auf 100 begrenzt. Das war auch gut so, ich mußte 81,5 Sekunden warten, bis sich der Ausschnitt aut dem Monitor zeigte.

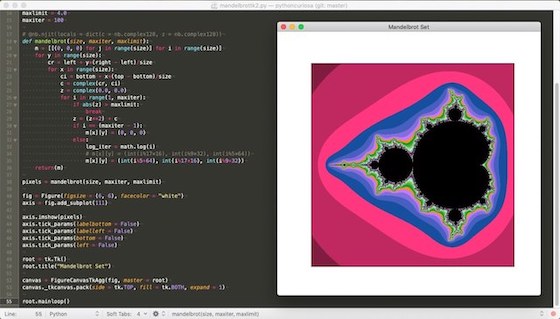
Die Bilder der Python-Version habe ich mit dem Matplotlib-Backend backend_tkagg und Tkinters Canvas auf den Monitor gezeichnet, da mir die Ausgabe im Matplotlib-Fenster (wie im sie im vorletzten Screenshot zu sehen ist) nicht gefiel. Es sah doch recht »altbacken« aus. Wie man die Matplotlib mit Tkinter verheiratet, habe ich hier beschrieben.

Da ich in Tkinter nicht so leicht wie in Processing auf den HSB-Farbraum zugreifen kann, habe ich der Einfachheit halber für die »simple« Farbpalette die RGB-Werte aus der Iterationstiefe berechnen lassen. Das dürfte den Geschwindigkeitsvergleich mit Processing.py höchstens unwesentlich verfälschen, nur die Farben sehen leicht anders aus. Die maximale Iterationstiefe habe ich hier ebenfalls auf 100 begrenzt.

Die vollständige Mandelbrotmenge erschien dann nach 14,4 Sekunden auf dem Monitor. Überraschung! Processing.py (und damit Jython) ist hier geringfügig schneller als (C)Python.

Auch hier natrlich das komplette Python-Skript:

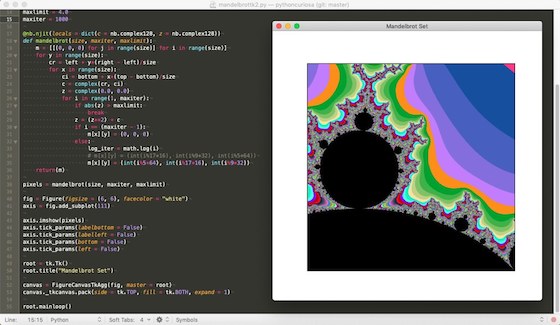
from matplotlib.figure import Figure
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
import tkinter as tk
import numpy as np
import numba as nb
import math

left   = -2.25
right  = 0.75
bottom = -1.5
top    = 1.5

size = 600
maxlimit = 4.0
maxiter = 100

# @nb.njit(locals = dict(c = nb.complex128, z = nb.complex128))
def mandelbrot(size, maxiter, maxlimit):
    m = [[(0, 0, 0) for j in range(size)] for i in range(size)]
    for y in range(size):
        cr = left + y*(right - left)/size
        for x in range(size):
            ci = bottom + x*(top - bottom)/size
            c = complex(cr, ci)
            z = complex(0.0, 0.0)
            for i in range(1, maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter - 1):
                    m[x][y] = (0, 0, 0)
                else:
                    log_iter = math.log(i)
                    # m[x][y] = (int(i%17*16), int(i%9*32), int(i%5*64))
                    m[x][y] = (int(i%5*64), int(i%17*16), int(i%9*32))
    return(m)

pixels = mandelbrot(size, maxiter, maxlimit)

fig = Figure(figsize = (6, 6), facecolor = "white")
axis = fig.add_subplot(111)

axis.imshow(pixels)
axis.tick_params(labelbottom = False)
axis.tick_params(labelleft = False)
axis.tick_params(bottom = False)
axis.tick_params(left = False)

root = tk.Tk()
root.title("Mandelbrot Set")

canvas = FigureCanvasTkAgg(fig, master = root)
canvas._tkcanvas.pack(side = tk.TOP, fill = tk.BOTH, expand = 1)

root.mainloop()

Für die späteren Versuche mit Numba habe ich Numba schon einmal importiert und den Decorator, der Numba aktiviert, für erste auskommentiert.

Nun war ich gespannt, wie Python im Vergleich mit Processing.py mit dem Ausscnitt fertig werden würde. Mit 23 Sekunden hatte dieses Mal (C)Python die Nase knapp vorne. Man kann vermuten, daß Python und Jython im Bezug auf die Geschwindigkeit ebenbürtig sind.

Nun meine Versuche mit der rechenintensiveren Farbpalette. Hier hatte bei der vollständigen Mandelbrotmenge Python wieder die Nase vorne: Nach 21,3 Sekunden konnte ich die Mandelbrotmenge auf meinem Monitor bewundern. Pythons math-Modul scheint gegenüber dem math-Modul von Jython doch etwas schneller zu sein.

Im Skript selber mußte ich dafür nur die for-Schleife in der Funktion mandelbrot() ändern:

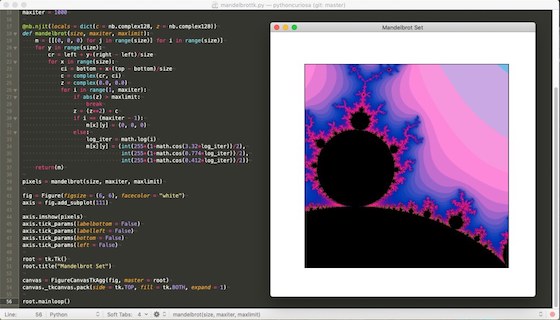
            for i in range(1, maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter - 1):
                    m[x][y] = (0, 0, 0)
                else:
                    log_iter = math.log(i)
                    m[x][y] = (int(255*(1+math.cos(3.32*log_iter))/2),
                               int(255*(1+math.cos(0.774*log_iter))/2),
                               int(255*(1+math.cos(0.412*log_iter))/2))

Doch dann das, auf das ich mich schon während der ganzen Experimente gefreut hatte: Ich will Geschwindigkeit! Also habe ich den Numba-Decorator eingeschaltet. Wow! Nach 4,7 Sekunden war das Programm durch.

Also habe ich todesmutig die maximale Iterationstiefe auf 1.000 erhöht. Numba ist immer noch unschlagbar, nur 9,2 Sekunden Rechenzeit und das Skript war wieder fertig.

Ähnlich waren die Ergebnisse dann auch bei dem Ausschnitt aus der Mandelbrotmenge: Bei auskommentierten Numba und einer maximalen Iterationstiefe von 100 brauchte das Skript 34,4 Sekunden. Das ist immerhin etwa doppelt so schnell, wie die Zeit von Processing.py. Das stärkt meine Vermutung, daß das math-Modul von Python 3 gegenüber dem math-Modul von Jython (das ja im Pronzip ein Python 2.7 ist) gewaltig die Nase vorn hat.

Und erst Numba: Bei einer maximalen Iterationstiefe von 100 hatte das Skript nach 5,9 Sekunden fertig, wenn ich die maximale Iterationstiefe auf 1.000 erhöhe, benötigte das Skript etwa die dreifache Zeit, nämlich 14,3 Sekunden. Übrigens waren zwischen den mit maximal 100 Iterationsschritten gezeichneten und den mit maximal 1.000 Iterationsschritten gezeichneten kaum Unterschiede festzustellen. Was die alte Volksweisheit bestätigt: Viel hilft nicht immer viel.

Zusammenfassung

Sieht man einmal davon ab, daß offenbar das math-Modul in Python 3 deutlich an Geschwindigkeit zugelegt hat, sind die Geschwindigkeits-Unterschiede zwischen Processing.py und Python 3 größtenteils vernachlässigbar. Setzt man aber Numba ein, dann sieht die Sache ganz anders aus: Die Rechenzeit schrumpft auf ein Viertel bis ein Siebtel der von Python ohne Numba benötigten Zeit.

Ankit Mahato hat in seinem Video Numba mit mehr oder weniger seltsamen Optimierungen noch weiter beschleunigt. Doch davon habe ich die Finger gelassen, denn teilweise litt die Lesbarkeit und Klarheit des Codes doch gewaltig darunter.

3 (Email-) Kommentare

Bei der Rechenleistung, die uns heute zur Verfügung steht, scheint mir selbst die Bestmarke von 4,7 Sekunden, die dein NumPy-Programm braucht, um die Mandelbrotmenge zu rendern, als viel zu lang.
Also das Ganze mal in Fortran umgesetzt, mit deinen Parametern (width: 600; height: 600; maxlimit: 4.0; maxiter: 100, left: -0.25; right: 0.25, top: -1.0; bottom: -0.5). Dann die Zeit gemessen, bis der Plot auf dem Bildschirm (X11) erscheint: 1,6 Sekunden (Core i5, 2.5 GHz). Screenshot ist im Anhang.
Die Geschwindigkeit hat aber weniger mit der Sprache als mit der Umsetzung zu tun: der Aufruf der Mandelbrot-Funktion lässt sich parallelisieren. In Python käme da u. a. asyncio in Frage, sofern man das Plotten vom Rendern trennt. Zudem sollte es schneller sein, die Ausgabe zunächst in einen Puffer zu schreiben, anstatt jeden Bildschirmpixel einzeln zu setzen. Den Puffer kann man dann in einem Aufruf auf den Bildschirm blitten. Mit den für Python verfügbaren Plotting-Tools kenne ich mich aber nicht hinreichend aus.

– Philipp (Kommentieren) (#)

Ich habe es jetzt nicht am Rechner nachvollzogen… aber das sieht mir danach aus als würdest Du bei jeder Iteration den Farbwert berechnen und das Pixel setzen. Das sind Operationen die in die Zeit gehen.
Das lässt sich vereinfachen indem zum setup die Berechnung einer Colorlookup table hinzugefügt wird und der Pixel erst gesetzt wird, wenn die Schleife durch ist.
Anbei ein Nodebox Skript, welches ohne Beschleuniger das Mandelbrötchen in unter 5Sek erzeugt.

– Karsten W. (Kommentieren) (#)

Das war Absicht. Ich wollte ja gerade sehen, in wieweit Numba gerade rechenintensive Operationen beschleunigt. Denn wer würde sonst bei jedem Schleifendurchlauf die Farbwerte mit Logarithmen und Cosinus-Werten berechnen? 🤓

– Jörg Kantel (Kommentieren) (#)

(Kommentieren)