Mathematik mit TigerJython: Das Lotka-Volterra-System

Ich möchte in der nächsten Zeit in loser Reihenfolge ein paar Beiträge zur Numerik schreiben und dafür TigerJython und das Modul GPanel zur Visualisierung verwenden. Ziel ist einmal, TigerJython besser kennenzulernen, vorrangig aber – da die bequemen numerischen Methoden aus NumPy nicht zur Verfügung stehen - sollen die verwendeten Algorithmen eigens entwickelt und programmiert werden. Ich will dabei keine hochkomplexe Numerik betreiben, sondern einfach ein paar Standardalgorithmen vorstellen, die jeder mal in der Programmiersprache seines Vertrauens implementiert haben sollte.

Den Anfang macht ein Klassiker, das Räuber-Beute-System nach Lotka-Volterra, ein System aus zwei nicht-linearen, gekoppelten Differentialgleichungen erster Ordnung. Sie beschreiben die Wechselwirkung von Räuber- und Beutepopulationen. Unter Räuber und Beute sind dabei zwei Klassen von Lebewesen gemeint, wobei die eine sich von der anderen ernährt (als Beispiel werden oft Hasen und Füchse genannt). Aufgestellt wurden die Gleichungen 1925 von Alfred J. Lotka und, unabhängig davon, 1926 von Vito Volterra. Mit Hilfe dieses Modells konnte damals die dramatische Abnahme des Sardinenfischfangs im Mittelmeer nach dem ersten Weltkrieg erklärt werden.¹

Die Gleichungen lauten²:

Dabei steht $B$ für die Anzahl der Beutetiere, $R$ für die Anzahl der Räuber $\epsilon{_1}$ ist die Reproduktionsrate der Beute, $\epsilon{_2}$ die Sterberate der Räuber, $\gamma{_1}$ steht für die Freßrate der Räuber (die im Modell gleichzeitig die Sterberate der Beute ist) und $\gamma{_2}$ ist die Reproduktionsrate der Raubtiere.³

Wenn man diese Differentialgleichungen mit dem Eulerschen Polygonzugverfahren lösen will, so kann man in Python folgende Zeilen schreiben:

B0 = 100 # Startwert Beutepopulation
R0 = 45  # Startwert Räuberpopulation

eps1 = 0.5      # Reproduktionsrate der Beute
gamma1 = 0.0333 # Freßrate der Räuber = Sterberate der Beute
eps2 = 1.0      # Sterberate der Räuber
gamma2 = 0.01   # Reproduktionsrate der Räuber

dt = 0.05       # delta time: Zeit- oder Iterationschritte
N = 1000        # N = Zahl der Iterationen

for n in range(N): 
    bNew = b + dt*(eps1*b - gamma1*b*r)
    rNew = r + dt*(-eps2*r + gamma2*b*r)
    # Plotte bNew und rNew
    b = bNew
    r = rNew

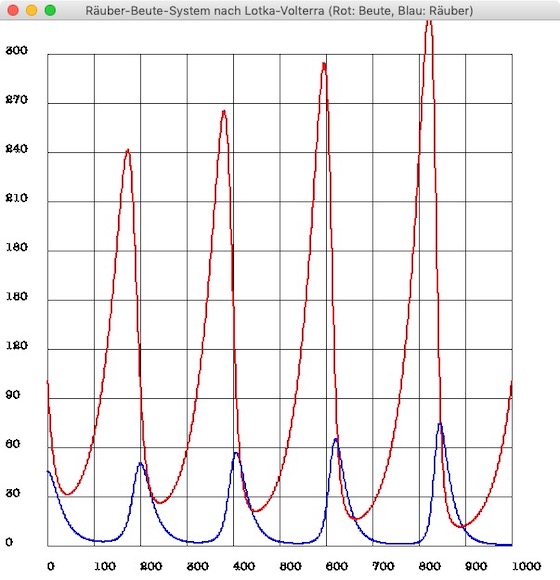
Wenn ich dieses System mit den obigen Parametern plotten lasse, so erhalte ich dieses Ergebnis:

Das überrascht ein wenig, denn nach der zweiten Lotka-Volterra-Regel sollte die Lösung periodisch sein, bei der man nach einer gewissen Zeitspanne – der Periodenlänge – den gleichen Systemzustand, das heißt die gleiche Anzahl an Beute und Raubtieren erhält. Danach wiederholt sich die Entwicklung, bis wieder eine Periodenlänge verstrichen ist, usw.⁴ Auf gar keinen Fall sollte das System überschwingen und im Laufe der Zeit in die Unendlichkeit entweichen.⁵

Daß das Ergebis anscheinend überschwingt, setzt nicht die zweite Lotka-Volterra-Regel außer Kraft, sondern zeigt, daß das angewendete Eulersche Polygonzugverfahren, das ja ein Näherungsverfahren ist, für dieses Problem nicht geeignet ist. Denn auch wenn man die Schrittweite dt kleiner wählt, steigt nur die Rechenzeit und die Überschwinungen werden geringer, verschwinden aber nie. Früher oder später entschwindet die Anzahl der Beutetiere und auch (wenn auch noch später) die Anzahl der Räuber im Nirwana der Unendlichkeit. Mit einem »magischen« Trick⁶ kann man das Überschwingen jedoch verhindern.

    bNew = b + dt*(eps1*b - gamma1*b*r)
    rNew = r + dt*(-eps2*r + gamma2*bNew*r)

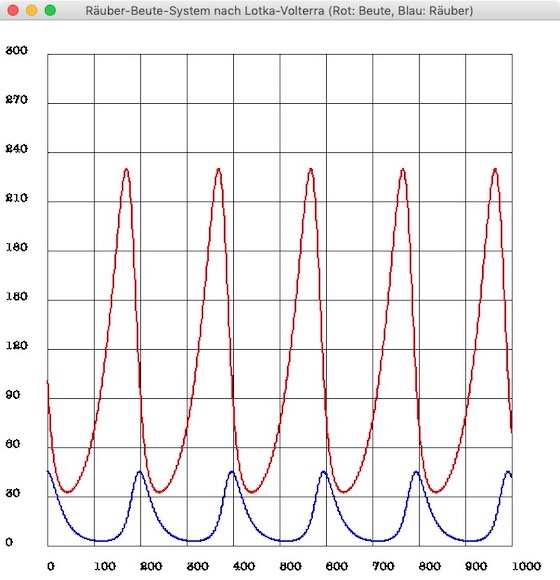
Denn setzt man in der Berechnung der zweiten Gleichung statt b das in der Zeile darüber schon berechnete bNew ein, dann verschwindet das Überschwingen wie von Zauberhand:

Das ist natürlich keine Zauberei, sondern diese Methode wird Euler-Cromer-Verfahren oder semi-implizietes Euler-Verfahren genannt. Während die erste Zeile in obigem Code einen Schritt in der Berechnung vorwärts macht, rechnet die zweite Zeile wieder einen Schritt zurück. Dieses Verfahren ist nicht hundertprozentig genau, man kann nachweisen, daß das System zwar seine Periodizität behält, aber nach (sehr) vielen Iterationsschritten sich die Perioden gegenüber einer exakten Lösung verlängern.

Für meine Zwecke bin ich aber mit dem Ergebnis des Euler-Cromer-Verfahrens zufrieden, denn numerische Lösungen sind immer Näherungslösungen und ich halte die gefundene Näherung für hinreichend genau.

Jetzt für alle, die es nicht erwarten können, ihr TigerJython anzuwerfen und zu programmieren, hier der komplette Quellcode:

# Lotka-Volterra-Gleichung mit dem Euler-Verfahren
# b = Beute
# r = Räuber

from gpanel import *

B0 = 100 # Startwert Beutepopulation
R0 = 45  # Startwert Räuberpopulation

eps1 = 0.5      # Reproduktionsrate der Beute
gamma1 = 0.0333 # Freßrate der Räuber = Sterberate der Beute
eps2 = 1.0      # Sterberate der Räuber
gamma2 = 0.01   # Reproduktionsrate der Räuber

dt = 0.05       # delta time: Zeit- oder Iterationschritte
N = 1000        # N = Zahl der Iterationen

myFont = Font("American Typewriter", Font.PLAIN, 12)

makeGPanel(-100, 1100, -20, 320)
title("Räuber-Beute-System nach Lotka-Volterra (Rot: Beute, Blau: Räuber)")
font(myFont)
drawGrid(0, 1000, 0, 300)

b = B0
r = R0

lineWidth(2)
for n in range(N):
    bNew = b + dt*(eps1*b - gamma1*b*r)
    # rNew = r + dt*(-eps2*r + gamma2*b*r)  # Explizites Euler-Verfahren
    rNew = r + dt*(-eps2*r + gamma2*bNew*r) # Euler-Cromer-Verfahren
    setColor("red")
    setColor("red")
    line(n, b, n + 1, bNew)
    setColor("blue")
    line(n, r, n + 1, rNew)
    b = bNew
    r = rNew

Das Python-Modul GPanel gibt es übrigens auch in einer Version für (C)Python. Damit wären dann Ausflüge mit NumPy und Scipy möglich. Aber warum sollte man dies machen, wenn einem dann doch die viel mächtigere Matplotlib zur Verfügung steht? Demgegenüber ist der Vorteil von TigerJython ja, daß ein Download reicht und es keine weiteren Abhängigkeiten gibt. Man kann TigerJython daher zwar nicht erweitern, aber meiner Meinung nach ist der gegebene Umfang zumindest für schulische Zwecke mehr als ausreichend.

(Kommentieren)