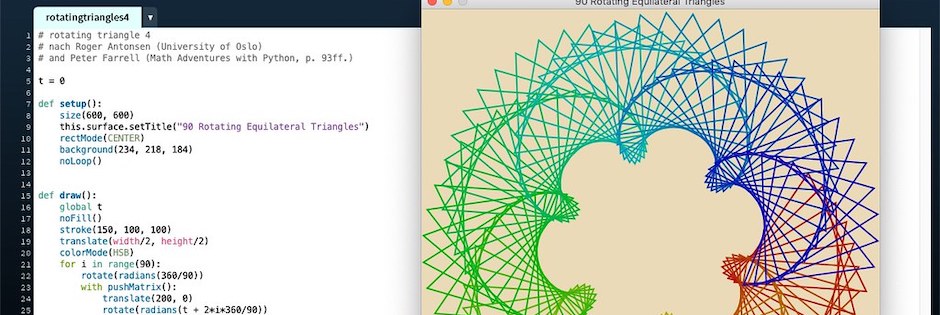
Programmier-Etüde: Rotierende Dreiecke mit Processing.py

Über Peter Farrells wunderbarem Buch »Math Adventures with Python« bin ich auf Roger Antonson von der Universität Oslo gestoßen, der auf seinen »Art«-Seiten sehr schöne Dinge mit Processing anstellt, unter anderem auch diese animierte Figur aus 90 rotierenden gleichseitigen Dreiecken. Peter Farrell inspierierte das zu einem ähnlichen Programm (Seite 93ff.) und auch ich wollte darauf aufbauend als Programmier-Etüde etwas Dekoratives in mein Processing.py-Fenster zaubern.

Doch zuerst möchte ich die Frage beantworten, warum bei der Konstruktion eines gleichseitigen Dreiecks die Formel $l\frac{\sqrt{3}}{2}$ auftaucht, die auch ich in meiner Funktion tri() verwende:

def tri(length):
    triangle(0, -length,
             -length*sqrt(3)/2, length/2,
             length*sqrt(3)/2, length/2)

Hier hilft – wie so häufig (nicht nur) in der Trigonometrie – der gute alte Lehrsatz des Pythagoras. Teilt man nämlich das gleichseitige Dreieck in drei flächengleiche Dreiecke im Mittelpunkt mit einer Senkrechten von der Spitze so erhält man sechs gleiche rechtwinklige Dreiecke. Der Einfachheit nehmen wir an, daß die Gegenkathete $a$ zum spitzen Winkel $\alpha$ ($30°$) die Länge $x$ besitzt, dann ist die Länge der Ankathete $b = 2x$. Für die Hypothenuse $c$ gilt dann $c^2=a^2+b^2$. Was wir wissen, ist die Länge der Ankathete $l$, da wir mit dieser Länge das gleichseitige Dreieck konstruieren. Dann beträgt die Länge der Gegenkathete $\frac{l}{2}$. Nun alles hübsch quadrieren und dann die Wurzel ziehen und schon haben wir die Länge der Hypothenuse, nämlich $l\frac{\sqrt{3}}{2}$. Wenn ich nun das Dreieck mit der Spitze nach Norden konstruiere und das Zentrum des Dreiecks in den Ursprung des Koordinatensystems $(0, 0)$ lege, dann besitzt die Spitze in der Mitte oben die Koordinaten $(0, -l)$, die Spitze unten links die Koordinaten $(-l\frac{\sqrt{3}}{2}, \frac{l}{2})$ und die Spitze rechts unten die Koordinaten $(l\frac{\sqrt{3}}{2}, \frac{l}{2})$. Damit ist die Konstruktion des Dreieckes geklärt.

Läßt man dieses Dreieck um den Ursprung rotieren, erhält man eine Art Kreis. Um eine ähnliche, wolkenartige Struktur wie in Roger Antonsons Figur zu bekommen, muß man der Rotation noch einen Phasenschub verpassen. Dazu nahm Farrell die Rotationsvariable t und die Laufvariable i. Damit die Figur »rund« abschließt, muß der Phasenschub ein Vielfaches von $360°$ betragen. Da 90 Dreiecke gezeichnet werden, kann man der Einfachheit halber t + 1 mit 360/90 multiplizieren, erhält also:

            rotate(radians(t + 2*i*360/90))

Natürlich weiß ich, daß $\frac{360}{90}=4$ ist, aber so ausgeschrieben, kann man die Formel einfacher ändern, wenn man die Anzahl der Dreiecke erhöht oder erniedrigt.

Jetzt aber für Neugierige der komplette Quellcode:

# rotating triangles 4
# after Roger Antonsen (University of Oslo)
# and Peter Farrell (Math Adventures with Python, p. 93ff.)

t = 0

def setup():
    size(600, 600)
    this.surface.setTitle("90 Rotating Equilateral Triangles")
    rectMode(CENTER)
    background(234, 218, 184)
    noLoop()

def draw():
    global t
    noFill()
    translate(width/2, height/2)
    colorMode(HSB)
    for i in range(90):
        rotate(radians(360/90))
        with pushMatrix():
            translate(200, 0)
            rotate(radians(t + 2*i*360/90))
            stroke(2*i, 255, 180)
            strokeWeight(2)
            tri(100)
    t += 0.5

def tri(length):
    triangle(0, -length,
             -length*sqrt(3)/2, length/2,
             length*sqrt(3)/2, length/2)

Wie man sieht, habe ich die Zeichnung aufgehübscht, in dem ich über Processings HSB-Mode das Regenbogen-Spektrum (erster Parameter H) durchlaufen habe. Bei voller Beleuchtung wurden die Farben allerdings für meinen Geschmack zu blaß, daher habe ich den dritten Paramter (Brightness B) auf 180 heruntergesetzt. Und mit strokeWeight(2) habe ich die Linien etwas fetter gemacht. So gefiel mir dann das Endergebnis (Screenshot).

Ich werde noch ein wenig in Peter Farrells Buch schmökern und ich glaube, es werden noch weitere Programmier-Etüden daraus entstehen. Still digging!

(Kommentieren)