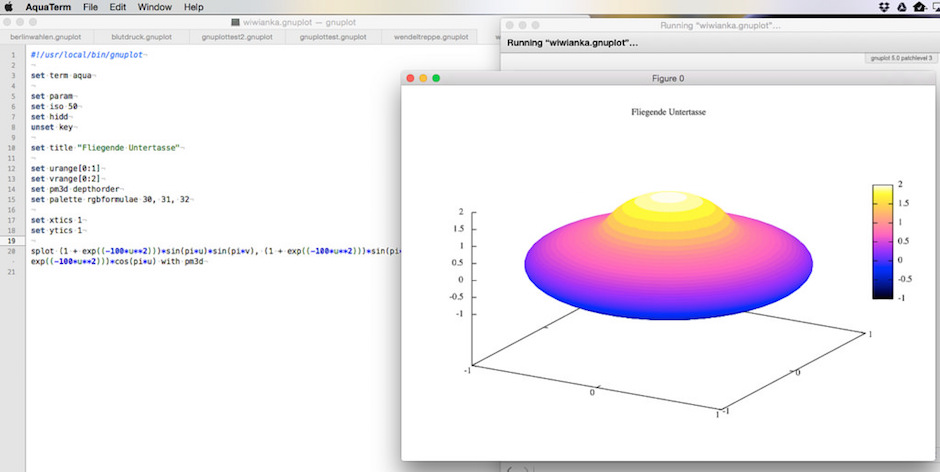
Spaß mit Gnuplot: Wir basteln uns eine fliegende Untertasse

Mit den parametrischen Oberflächen in 3D von Gnuplot kann man schon einiges seltsames anstellen. Sich zum Beispiel eine fliegende Untertasse zusammenbasteln. Die Formel dafür ist ganz schön kompliziert:

x = (1 + exp((-100*u**2)))*sin(pi*u)*sin(pi*v)
y = (1 + exp((-100*u**2)))*sin(pi*u)*cos(pi*v)
z = (1 + exp((-100*u**2)))*cos(pi*u) with pm3d

Dabei gilt 0 <= u <= 1 und 0 <= v <= 1. Das heißt, u durchläuft die Werte zwischen 0 und 1 und v die Werte zwischen 0 und 2. Das Gnuplot-Skript unterscheidet sich ansonsten nicht wesentlich von dem letzten:

set term aqua

set param
set iso 50
set hidd
unset key

set title "Fliegende Untertasse"

set urange[0:1]
set vrange[0:2]
set pm3d depthorder
set palette rgbformulae 30, 31, 32

set xtics 1
set ytics 1

splot (1 + exp((-100*u**2)))*sin(pi*u)*sin(pi*v),
      (1 + exp((-100*u**2)))*sin(pi*u)*cos(pi*v),
      (1 + exp((-100*u**2)))*cos(pi*u) with pm3d

Die splot-Zeile habe ich der besseren Lesbarkeit wegen umgebrochen, im Skript muß natürlich alles in einer Zeile stehen.

Clifford A. Pickover hat in seinem Buch Mazes for the Mind – Computers and the Unexpected, New York (St. Martins Press) 1992, Seite 97-99 die Figur Wiwianka Oberfläche (Wiwianka Surface) genannt, nach dem Mathematiker Waldemar Wiwianka, der sie als erstes beschrieben haben soll.

Mit rgbformulae Paletten zu setzen, ist leider wenig intuitiv. Ich habe die Palette daher einfach von diesen Seiten geklaut. Sie beantworten generell viele Fragen, die man zu Gnuplot haben könnte.

(Kommentieren)