Schockwellenreiter: Shoes zieht Kreise

Schockwellenreiter → Archiv → Mai 2016 → Shoes zieht Kreise – 20160503

Shoes zieht Kreise

Punkte, Kästchen, Linien und Kreise sind die Grundelemente, mit denen man in Shoes, dem plattformübergreifenden, kleinen Ruby-Toolkit für GUIs und 2D-Graphiken Zeichnungen erstellen kann. Ich möchte sie hier im Schockwellenreiter im Rahmen meiner Shoes-Reihe successive mit kleinen Beispielskripten vorstellen und fange mit Kreisen (und Ovalen) an.

Shoes hat sich bei diesen Shapes sehr stark von Nodebox inspirieren lassen, das wiederum sich seine Ideen von Processing ausgeborgt hat. Dennoch macht Shoes einiges anders, zum Beispiel bei Farben und es erlaubt auch Bilder und Gradienten als fill für Linien und Objekten.

Um einen einfachen Kreis zu zeichnen, benötigt man folgendes Skript:


Shoes.app width: 500, height: 500, title: "Einfacher Kreis", resizable: false do
  stroke black
  strokewidth 2
  fill red
  oval width/2, height/2, 250, center: true
end

Die Syntax für einen Kreis ist

oval(x, y, radius)

Dabei ist – im Gegensatz zu dem, was das Manual behauptet – mit radius nicht der Radius, sondern der Druchmesser des Kreises gemeint. Diese Verwirrung hat bei mir anfangs zu einiger Irritation geführt.

Will man eine Ellipse zeichnen, kommt ein weiterer Parameter hinzu

oval(x, y, width, height)

und dann wird klar, daß mit radius tatsächlich nur der Durchmesser gemeint sein kann.

Per Default sind die x- und y-Koordinaten des Kreises die obere linke Ecke. Das ist zum Beispiel günstig, wenn man ein Go- oder Damespiel auf einem Brett programmieren oder einen zellulären Automaten mit Kreisen als Zellen zeichnen will. Jedoch ist es für andere Dinge oftmals günstiger, die x- und y-Koordinaten in den Mittelpunkt des Kreises zu legen. Das erreicht man, indem man mit

center: true

die x- und y-Koordinaten transformiert.

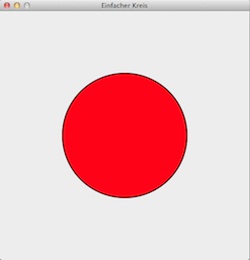
Mit stroke black, strokewidth 2 und fill red habe ich Shoes mitgeteilt, daß der Kreis einen schwarzen, zwei Pixel breiten Rand und eine rote Füllung haben soll. Das Ergebnis zeigt der nebenstehende Screenshot.

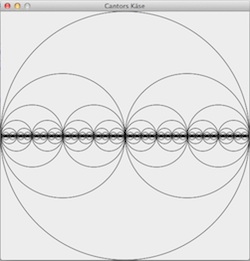
Einfache Kreise oder Ellipsen zu zeichnen, ist natürlich ein wenig langweilig. Aber selbst damit kann man schon interessante Muster erzeugen, wie zum Beispiel den Cantor-Käse, eine Figur, die der Cantor-Menge topologisch ähnlich ist. Sie wird konstruiert, in dem aus einem Kreis bis auf zwei kleinere Kreise alles entfernt wird. Aus diesen zwei kleineren Kreisen wird wiederum bis auf zwei kleinere Kreise alles entfernt. Nun hat man schon vier Kreise, aus denen man jeweils bis auf zwei kleinere Kreise alles entfernt. Und so weiter und so fort …

Das schreit natürlich nach einer rekursiven Funktion und die sieht so aus:


Shoes.app width: 500, height: 500, title: "Cantors Käse", resizable: false do
  strokewidth 1
  nofill
  
  def cheese(x, y, r, level)
    oval x, y, r, center: true
    if level > 1
      cheese(x - r/4, y, r/2, level-1)
      cheese(x + r/4, y, r/2, level-1)
    end
  end
  
  cheese(250, 250, 500, 10)
end

Und wieder zeigt der nebenstehende Screenshot das Ergebnis.

Bei Rekursionen in Shoes scheint man vorsichtig sein zu müssen. Die obige Rekursionstiefe von 10 wird noch problemlos abgearbeitet, bei einer Rekursionstiefe von 12 gerät das Skript schon leicht ins Stottern und bei einer Rekursionstiefe von 15 stürzt Shoes gnadenlos ab. Rekursionen sind bekanntlich speicherhungrig und vermutlich müßte man Shoes mehr Arbeitsspeicher zuweisen. Leider weiß ich aber nicht, wie man das anstellt, vielleicht kann mir jemand von Euch da draußen weiterhelfen.

Der in der Literatur anzutreffende Pseudocode für einen Kantor-Käse sagt natürlich


  def cheese(x, y, r, level)
    oval x, y, r, center: true
    if level > 1
      cheese(x - radius/2, y, frac*radius, level-1)
      cheese(x + radius/2, y, frac*radius, level-1)
    end
  end

Dabei ist mit radius natürlich der echte Radius der Kreise gemeint und frac ist eine Zahl mit 0.0 > frac <= 0.5.

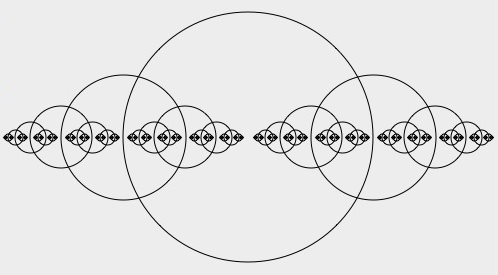
Setzt man diesen Pseudocode naiv eins zu eins in Shoes um, ohne die seltsame Vorstellung, die Shoes vom Radius eines Kreises hat, zu berücksichtigen, erhält man folgendes Skript


Shoes.app width: 500, height: 500, title: "Das ist kein Cantor-Käse", resizable: false do
  strokewidth 1
  nofill
  
  def cheese(x, y, r, level)
    oval x, y, r, center: true
    if level > 1
      cheese(x - r/2, y, r/2, level-1)
      cheese(x + r/2, y, r/2, level-1)
    end
  end
  
  cheese(250, 250, 250, 10)
end

das zwar keinen Cantor-Käse, aber ebenfalls eine ansprechende, nett aussehende Figur zeichnet:

Literatur

Clifford A. Pickover: Mit den Augen des Computers. Phantastische Welten aus dem Geist der Maschine, München (Markt und Technik) 1992. Diese deutsche Übersetzung von Computers and the Imagination ist eine geniale Fundgrube für alle, die Simulationen und mathematische Spielereien mit dem Computer lieben. Es ist eines der besten Bücher Pickovers. Dem Cantor-Käse ist auf den Seiten 171-181 ein eigenes Kapitel gewidmet.
Chris Robart: Programming Ideas: For Teaching High School Computer Programming, ( 260 KB, 2nd Edition) 2001. Ebenfalls eine Fundgrube voller Ideen, deren Download sich in jedem Fall lohnt.

Mehr Schuhe im Schockwellenreiter

(Kommentieren)