Schockwellenreiter: Als die Computerwelt noch schwarz-weiß war

Schockwellenreiter → Archiv → Februar 2019 → Als die Computerwelt noch schwarz-weiß war – 20190219

Computergeschichte(n) mit Python: Als die Welt noch schwarz-weiß war

Als die Computerwelt noch jung war – also bis in die 1970er Jahre – gab es zumindest für Normalsterbliche, die keinen Zugang zu teuren Plottern hatten, kaum eine Möglichkeit, Computergraphiken auszugeben. Monitore wie auch Drucker waren in der Regel für die Ausgabe von Buchstaben ausgelegt und diese waren auf 80 Zeichen in der Breite begrenzt. Das berüchtigte Endlospapier mit den grünen Linien schaffte – glaube ich – 120 Zeichen pro Zeile, aber hier kann mich meine Erinnerung täuschen. Und die Welt war schwarz-weiß, denn auch auf die Ausgabe von Graustufen mußte man verzichten.

ASCII-A[k|r]t

Aber der Mensch ist ja erfinderisch und so kam man bald auf die Idee, die Buchstaben für die Ausgabe von Zeichnungen zu verwenden. Einmal »seriös« als die Diagramme und Graphen, aber auch sehr viele Comic-Bildchen und andere Strichzeichnungen wurden populär. So gab schon 1960 der Compiler der von Algol 58 beeinflußten Sprache MAD (Michigan Algorithm Decoder) in einigen frühen Versionen bei zu vielen Programmierfehlern ein Portrait von Alfred E. Neumann dem Maskottchen der Satirezeitschrift Mad aus, mit der Bemerkung »What Me Worry« (Bildquelle: Wikimedia Commons)

Auch hier ist schon der Versuch festzustellen, durch unterschiedliche Zeichen mit ihren unterschiedlichen Dichten »Graustufen zu simulieren« (wenn auch dies vermutlich eher satirisch gemeint war).

Ich möchte Euch ewin ähnliches Verfahren vorstellen, daß ein farbiges Bild in Graustufen wandelt und diese Graustufen dann durch unter unterschiedliche Buchstaben/Symbole näherungsweise darzustellen versucht. Dafür sind einige Schritte erforderlich:

Konvertiere das Bild in Graustufen – das habe ich mit der PIL/Pillow-Funktion convert("L") erledigt.
Teile das Bild ein ein Gitterraster (MxN) auf, das der Höhe des verwendeten Fonts entspricht (die Zeilenbreite N habe ich mit 80 Zeichen konstant gesetzt).
Berechne die Anzahl der Zeilen M um das Seitenverhältnis korrekt zu setzen (hier muß ich gestehen, ich habe einfach gespielt, bis ich einen Aspekt-Ratio von 0.45 (scale) als akzeptabel gefunden habe).
Berechne den durchschnittlichen Grauwert jedes einzelnen Rasters und weise ihm dann einen Buchstaben zu.
Schreibe jede Zeile als String in eine Datei, bis das Bild abgearbeitet ist.

Für die Graustufen habe ich zwei Zeichensätze ausgewählt, einmal einen mit 70 und einmal einen mit 10 Grauschattierungen:

# 70 Shades of Gray:
gscale1 = "$@B%8&WM#*oahkbdpqZO0QLCJUYXzcvunxrjft/\|()1{}[]?-_+~<>i!lI;:,\"^`'´. "

# 10 Shades of Gray
gscale2 = "@%#*+=-:. "

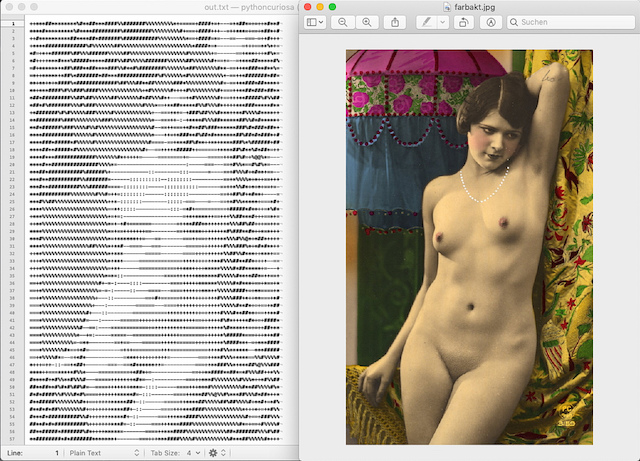
Diese Abstufungen sind nicht auf meinem eigenen Mist gewachsen, sondern ich habe sie dem Beitrag »Character representation of grey scale images« von Paul Bourke aus dem Jahre 1997 entnommen. Im Falle des von mir ausgewählten Aktbildchens, das schon in anderen Zusammenhängen Verwendung fand, stellte sich heraus, daß die Verwendung von nur 10 Graustufen das bessere Ergebnis brachte:

Man muß schon viel Phantasie aufbringen – oder sehr weit zurücktreten – um den Zusammenhang zum Originalbild zu erkennen, aber damals hatte man ja kaum eine andere Möglichkeit. Und so zierten solche und ähnliche Bilder viele Büros von SysAdmins.

Hier der komplette Quellcode:

import numpy as np
import os
from PIL import Image

# Parameter
in_file = "farbakt.jpg"
out_file = "out.txt"
scale = 0.45
cols = 80
more_levels = False

file_path = os.path.dirname(os.path.abspath(__file__))
image_folder = os.path.join(file_path, "images")

# Graustufenskalen aus: Paul Bourke: Character representation of grey scale images
# http://paulbourke.net/dataformats/asciiart/

# 70 Shades of Gray:
gscale1 = "$@B%8&WM#*oahkbdpqZO0QLCJUYXzcvunxrjft/\|()1{}[]?-_+~<>i!lI;:,\"^`'´. "

# 10 Shades of Gray
gscale2 = "@%#*+=-:. "

def get_average(image):
    im = np.array(image)
    w, h = im.shape
    return(np.average(im.reshape(w*h)))

def convert_image_to_ascii(file_name, cols, scale, more_levels):
    # Bilddatei öffnen und zu Graustufen konvertieren
    image_path = os.path.join(image_folder, file_name)
    image = Image.open(image_path).convert("L")
    W, H = image.size[0], image.size[1]
    w = W/cols
    h = w/scale
    rows = int(H/h)
    ascii_img = []
    for j in range(rows):
        y1 = int(j*h)
        y2 = int((j + 1)*h)
        # Sonderbehandlung für das letzte Reihe
        if j == rows - 1:
            y2 = H
        ascii_img.append("")
        for i in range(cols):
            x1 = int(i*w)
            x2 = int((i + 1)*w)
            # Sonderbehandlung für die letzte Spalte
            if i == cols - 1:
                x2 = W
            img = image.crop((x1, y1, x2, y2))
            avg = int(get_average(img))
            if more_levels:
                gsval = gscale1[int((avg*69)/255)]
            else:
                gsval = gscale2[int((avg*9)/255)]
            ascii_img[j] += gsval
    return(ascii_img)
    
aimg = convert_image_to_ascii(in_file, cols, scale, more_levels)
f = open(out_file, "w")
for row in aimg:
    f.write(row + "\n")
f.close()
print("I did it, Babe!")

Zufallsschwellwert

Und dann kamen auf einmal graphikfähige Monitore auf den Markt, die teillweise sogar bunt (16 oder 255 Farben) konnten, dies aber nur in einer sehr geringen Auflösung. Legendär waren aber die schwarz-weiß-Bildschirme von Apple SE 30 (512x342 Bildpunkte), des Atari (640x400 Bildpunkte) und die berühmte Hercules-Graphik auf dem PC mit sagenhaften 720x348 Pixeln. Alle diese Pixelangaben beziehen sich aber auf 1-Bit-Graphiken, die Monitore konnten in dieser Auflösung also tatsächlich nur entweder schwarze oder weiße Punkte darstellen. Aber man konnte einzelne Pixel ansprechen und so kam man schon früh auf die Idee, Graustufen durch ein Raster unterschiedlicher Pixeldichten zu simulieren. Denn das war nicht nur für die Darstellung auf dem Monitor wichtig, sondern auch für die Publikation: (Nadel-) Drucker wie auch Photokopierer konnten ebenfalls keine Graustufen, sondern nur schwarz-weiß. Dafür wurden unterschiedliche Verfahren entwickelt und diese Algorithmen nannte man Dithering.

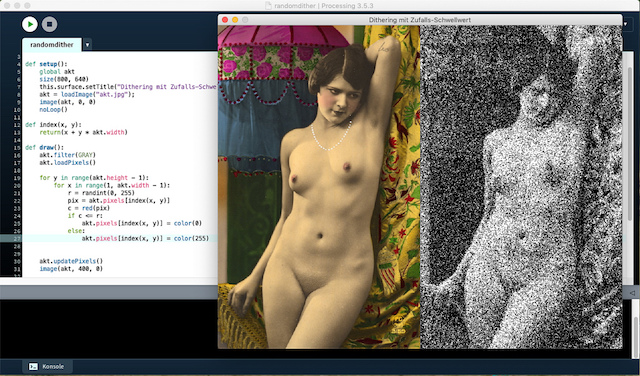
Eines der frühesten Verfahren war die Zufallskodierung. Für jeden Bildpunkt wird eine Zufallszahl r erzeugt, dei im Intervall [0, 255] gleichverteilt sein muß. Ein schwarzer Punkt wird nur dann ausgegebn falls sein Wert s(x, y) <= r ist. Dieses Verfahren, das sehr einfach zu implementieren ist, kann mit der Spritztechnik »mit Pinsel oder Zahnbürste« verglichen werden, mit der in meiner Jungend so ziemlich alle Schülerinnen und Schüler im Kunstunterricht gequält wurden.

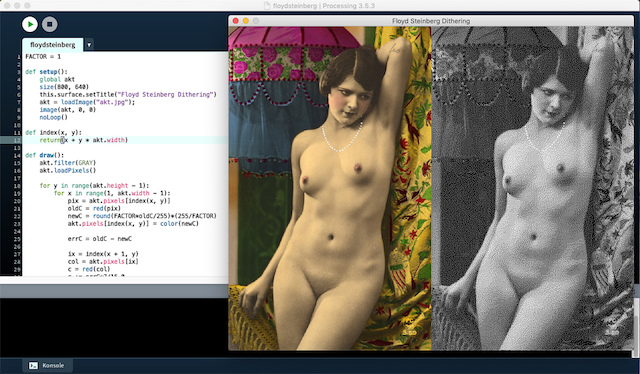
Ich habe dieses und die folgenden beiden Verfahren in Processing.py, dem Python-Mode von Processing implementiert. Das Programm für den Zufallsschwellwert ist sehr einfach und das Ergebis zeigt der obige Screenshot:

from random import randint

def setup():
    global akt
    size(800, 640)
    this.surface.setTitle("Dithering mit Zufalls-Schwellwert")
    akt = loadImage("akt.jpg");
    image(akt, 0, 0)
    noLoop()

def index(x, y):
    return(x + y * akt.width)
    
def draw():
    akt.filter(GRAY)
    akt.loadPixels()
    
    for y in range(akt.height):
        for x in range(akt.width):
            r = randint(50, 255)
            pix = akt.pixels[index(x, y)]
            c = red(pix)
            if c <= r:
                akt.pixels[index(x, y)] = color(0)
            else:
                akt.pixels[index(x, y)] = color(255)
    

    akt.updatePixels()
    image(akt, 400, 0)

Ein Trick ist, daß ich – nachdem ich das Bild zu einem Graustufenbild konvertiert habe, ich mir nur noch den roten Farbkanal anschaue. Denn bei einem Graustufenbild haben alle Kanäle im RGB-Farbraum den gleichen Wert, ein mittleres Grau wäre also (120, 120, 120).

Multischwellwertverfahren

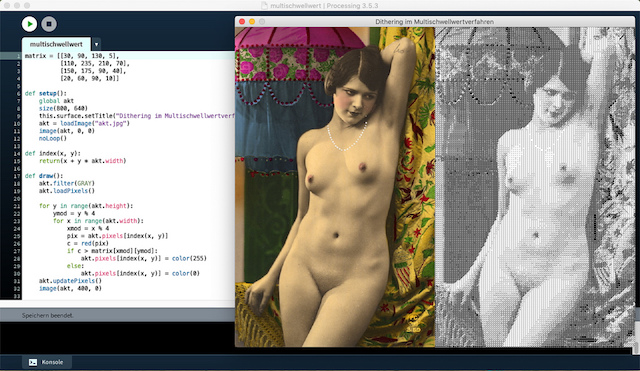
Zugegeben, das Zufallsverfahren ist immer noch nicht wirklich das »Gelbe vom Ei«, aber man konnte wenigstens erkennen, was das Bild darstellen sollte. Eine Verbesserung brachte dann das Multischwellwert-Dithering. Hier wird eine 4x4-Matrix (Dithermatrix) von Schwellwerten vorgegeben, etwa:

matrix = [[30, 90, 130, 5],
          [110, 235, 210, 70],
          [150, 175, 90, 40],
          [20, 60, 90, 10]]

Bei der Ausgabe eines Bildpunktes an der Position (x, y) werden zu den Koordinatenwerten die Größen

xmod = x % 4
ymod = y % 4

berechnet. Die Werte xmod und ymod liegen immmer zwischen null und drei und dienen der Positionsangabe in der Schwellwertmatrix. Für den Grauwert s(x, y) wird dann ein schwarzer Punkt ausgeben, wenn er kleiner ist als der Schwellwert in der Schwellwertmatrix in der Position (xmod, ymod), sonst wird kein schwarzer Punkt ausgegeben.

Das Verfahren entsprach einem Rasterverfahren, das zur damaligen Zeit bei der Ausgabe von Halbtonbildern in Druckereien verwendet wurde und lieferte, wie auch der Screenshot zeigt, schon recht ansprechende Ergebnisse, die sich auch gut zur Vervielfältigung auf den damaligen Photokopiergeräten eigneten.

Auch dieses Verfahren habe ich in Processing.py implementiert:

matrix = [[30, 90, 130, 5],
          [110, 235, 210, 70],
          [150, 175, 90, 40],
          [20, 60, 90, 10]]

def setup():
    global akt
    size(800, 640)
    this.surface.setTitle("Dithering im Multischwellwertverfahren")
    akt = loadImage("akt.jpg")
    image(akt, 0, 0)
    noLoop()

def index(x, y):
    return(x + y * akt.width)

def draw():
    akt.filter(GRAY)
    akt.loadPixels()

    for y in range(akt.height):
        ymod = y % 4
        for x in range(akt.width):
            xmod = x % 4
            pix = akt.pixels[index(x, y)]
            c = red(pix)
            if c > matrix[xmod][ymod]:
                akt.pixels[index(x, y)] = color(255)
            else:
                akt.pixels[index(x, y)] = color(0)
    akt.updatePixels()
    image(akt, 400, 0)

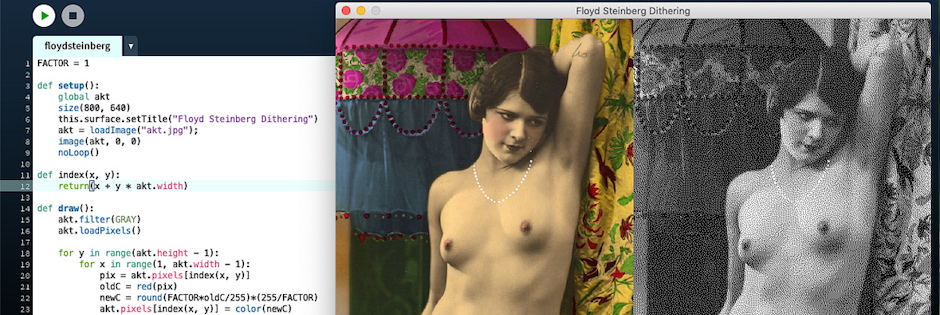
Floyd-Steinberg Dithering

Der Algorithmus liefert für seine Kürze und seine Einfachheit schon wirklich gute Ergebnisse, wenn auch die durch die Dithermatrix vorgegebenen erkennbaren Wiederholungen von Pixel-Mustern ein wenig störten. Man konnte dies zwar durch größere Dithermatrixen etwas mildern, aber sie waren Teil des Algorithmus und daher nicht auszumerzen. Bis dann 1976 die berühmten Informatiker Robert W Floyd und Louis Steinberg einen nach ihnen benannten Dithering-Algorithmus veröffentlichten. Dieser Algorithmus arbeitet nach einem Fehlerdiffusionsverfahren (error diffusion), das heißt der bei der Quantisierung auftretende Fehler (die Differenz zwischen Ausgangswert und quantisiertem Wert) eines jeden Pixels wird nach einem festen Schema auf die umliegenden Pixel verteilt. Dadurch vermied er die starre Maske, wie sie durch die festen Matrizen des Multischwellwertverfahrens vorgegeben waren.

Das Geniale war aber, daß durch das Schema, wie die Fehler auf die umliegenden Pixel verteilt wurden,

	P	⁷⁄₁₆
³⁄₁₆	⁵⁄₁₆	¹⁄₁₆

nur die Pixel angesprochen wurden, die nach dem aktuellen Pixel auftraten. Dadurch kann der Algorithmus ohne separaten Puffer die gesamte Eingabe in einem einzigen Durchlauf abarbeiten. Bereits verarbeitete Pixel werden nicht geändert, während noch abzuarbeitende Pixel entsprechend den auftretenden Quantisierungsfehlern beeinflußt werden.

In Porcessing.py formuliert sieht das so aus:

FACTOR = 1

def setup():
    global akt
    size(800, 640)
    this.surface.setTitle("Floyd Steinberg Dithering")
    akt = loadImage("akt.jpg");
    image(akt, 0, 0)
    noLoop()

def index(x, y):
    return(x + y * akt.width)
    
def draw():
    akt.filter(GRAY)
    akt.loadPixels()
    
    for y in range(akt.height - 1):
        for x in range(1, akt.width - 1):
            pix = akt.pixels[index(x, y)]
            oldC = red(pix)
            newC = round(FACTOR*oldC/255)*(255/FACTOR)
            akt.pixels[index(x, y)] = color(newC)
            
            errC = oldC - newC
            
            ix = index(x + 1, y)
            col = akt.pixels[ix]
            c = red(col)
            c += errC*7/16.0
            akt.pixels[ix] = color(c)
            
            ix = index(x - 1, y + 1)
            col = akt.pixels[ix]
            c = red(col)
            c += errC*3/16.0
            akt.pixels[ix] = color(c)

            ix = index(x, y + 1)
            col = akt.pixels[ix]
            c = red(col)
            c += errC*5/16.0
            akt.pixels[ix] = color(c)

            ix = index(x + 1, y + 1)
            col = akt.pixels[ix]
            c = red(col)
            c += errC*1/16.0
            akt.pixels[ix] = color(c)

    akt.updatePixels()
    image(akt, 400, 0)

FACTOR ist eine Konstante, die die Anzahl der möglichen Grauwerte festlegt, denn der Algorithmus funktioniert nicht nur für reine 1-Bit-Bilder, sondern es können mit FACTOR = 3 zum Beispiel auch vier Grauwerte ausgegeben werden. Und wenn die RGB-Felder separat berechnet werden, sind auch farbreduzierte Bilder möglich. Daniel Shiffman hat das in seinem Video zum Floyd-Steinberg-Dithering sehr schön gezeigt, aber ich bin in meinem Beispiel davon ausgegangen, daß ein reines Schwarz-Weiß-Bild erzeugt werden soll, wie man es damals auf den Monitoren von Apple, Atari und den Hercules-Bildschirmen hatte.

Man muß wirklich schon genau hinschauen, um die Rasterung noch zu erkennen. Das menschliche Auge läßt sich nämlich leicht überlisten und sieht ab einem gewissen Augenabstand vom Bild tatsächlich nur noch Graustufen.

Damit habe ich meinen kleinen Ausflug in die Vergangenheit der Computergraphik beendet. Vielleicht bringe ich in späteren Beispielen noch mehr Computergeschichten, programmiert in Python. Schaun wir mal …

Literatur

Peter Haberäcker: Digitale Bildverarbeitung. Grundlagen und Anwendungen, München, Wien (Hanser) 4. Auflage 1991
Jörg Kantel: SLIP. Eine Sprache zwischen den Stühlen, in: Marianne Baranovska/Stefan Höltgen (Hg): Hello, I’m Eliza. Fünfzig Jahre Gespräche mit Computern, Computer Archäologie, Band 4, Bochum, Freiburg (projektverlag) 2018, Seiten 73-87
Mahesch Venkitachalam: Python Playground. Geeky Projects for the Curious Programmer, San Francisco (no starch press) 2016

(Kommentieren)