Noch einmal die Lotka-Volterra-Gleichungen, nun in Python

Aus reiner Neugier habe ich die Lotka-Volterra-Gleichungen auch einmal in Python implementiert. Gefällt mir beinahe besser als die Maxima-Version. Aber das kann natürlich daran liegen, daß ich mich in Python zu Hause fühle und Maxima neu für mich ist.

Der große Unterschied zur (interaktiven) Maxima-Version ist der, daß ich das Gleichungssystem als Funktion implementiert habe. Daher konnte ich vorab die Parameter als Variablen angeben, was mehr Komfort verspricht, wenn man mit den Parametern spielen möchte.

# Parameter

eps1 = 0.5      # Reproduktionsrate der Beute
gamma1 = 0.0333 # Freßrate der Räuber = Sterberate der Beute
eps2 = 1.0      # Sterberate der Räuber
gamma2 = 0.01   # Reproduktionsrate der Räuber

def deriv(u, t, eps1, eps2, gamma1, gamma2):
    x, y = u
    dBdt = eps1*x - gamma1*x*y
    dRdt = -eps2*y + gamma2*x*y
    return(dBdt, dRdt)

Für die (numerische) Integration der Differentialgleichungen mußte das gute, alte odeint() aus dem Modul scipy ran, das auf die ebenso gute, aber noch ältere FORTRAN-Bibliothek ODEPACK (erste Implementierung 1983) zugreift. Diese dürfte über die Jahre so ausgereift und fehlerfrei sein, daß es da nichts mehr zu bemängeln gibt (darum lieben Numeriker die guten alten FORTRAN-Bibliotheken LAPACK, ODEPACK, etc.).

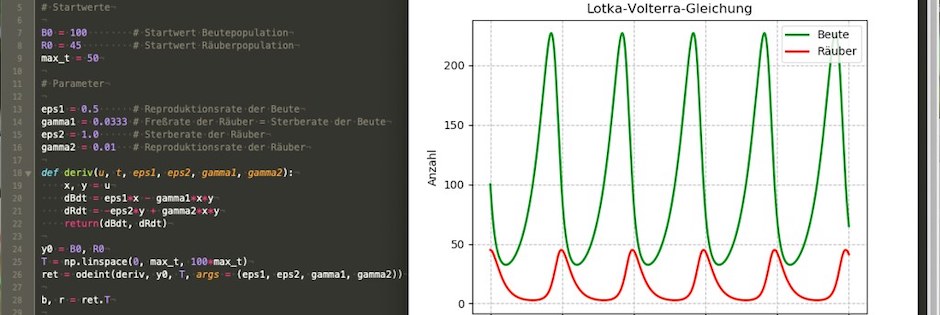
Für Nachahmer hier das komplette Programm (oder besser Progrämmchen):

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# Startwerte

B0 = 100        # Startwert Beutepopulation
R0 = 45         # Startwert Räuberpopulation
max_t = 50

# Parameter

eps1 = 0.5      # Reproduktionsrate der Beute
gamma1 = 0.0333 # Freßrate der Räuber = Sterberate der Beute
eps2 = 1.0      # Sterberate der Räuber
gamma2 = 0.01   # Reproduktionsrate der Räuber

def deriv(u, t, eps1, eps2, gamma1, gamma2):
    x, y = u
    dBdt = eps1*x - gamma1*x*y
    dRdt = -eps2*y + gamma2*x*y
    return(dBdt, dRdt)

y0 = B0, R0
T = np.linspace(0, max_t, 100*max_t)
ret = odeint(deriv, y0, T, args = (eps1, eps2, gamma1, gamma2))

b, r = ret.T

plots = plt.plot(T, b, "g", lw = 2, label = "Beute") \
        + plt.plot(T, r, "r", lw = 2, label = "Räuber")
plt.title("Lotka-Volterra-Gleichung")
plt.xlabel("Zeit [Tage]")
plt.ylabel("Anzahl")
plt.grid(True, linestyle = "--")
plt.legend(loc = "upper right")

plt.show()

Von den Lotka-Volterra-Gleichungen gibt es diverse Variationen und Erweiterungen (zum Beispiel mehrere Beutetiere oder mehrere Arten von Räubern oder Beutetiere mit begrenzter Weidekapazität). Wenn ich in meiner Bibliothek die Literatur dazu (wieder-) finde, werde ich eventuell noch einmal darauf zurückkommen. Still digging!

(Kommentieren)