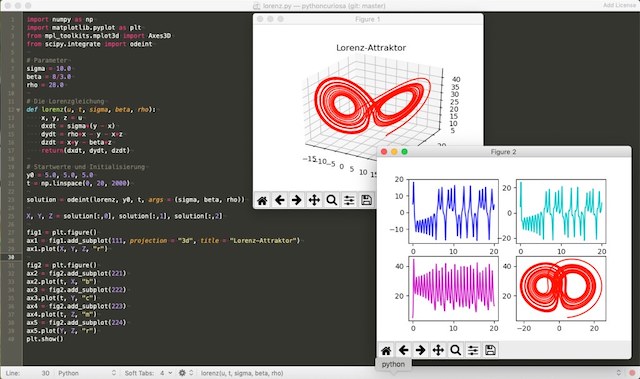
Der Lorenz-Attraktor mit Python, Numpy, scipy und der Matplotlib

Den Lorenz-Attraktor hatte ich schon zwei mal hier im Blog Kritzelheft behandelt: Einmal (um 2013) hatte ich ihn in R implementiert, um zu testen, ob R als Simulationsplattform taugt, und ein zweites Mal (im Juni 2017) hatte ich ihn in Processing.py, dem Python-Mode von Processing, programmiert. In beiden Artikeln findet Ihr auch mehr Hintergrundinformationen zu diesem »seltsamen Attraktor«.

Dieses Mal geht es mir weniger um den Attraktor selber, sondern mehr um die Frage, was man mit Pythons Matplotlib so alles anstellen kann. Mein Ziel war, zwei Plotfenster gleichzeitig offen zu haben, eines mit einem 3D-Plot und ein zweites mit mehreren 2D-Plots zum Vergleich.

Wie obiger Screenshot zeigt, geht das und es tut noch nicht einmal weh. Schlüssel dazu ist der objektorientierte Ansatz über zwei figure-Objekte.

fig1 = plt.figure()
ax1 = fig1.add_subplot(111, projection = "3d", title = "Lorenz-Attraktor")
ax1.plot(X, Y, Z, "r")

fig2 = plt.figure()
ax2 = fig2.add_subplot(221)
ax2.plot(t, X, "b")
ax3 = fig2.add_subplot(222)
ax3.plot(t, Y, "c")
ax4 = fig2.add_subplot(223)
ax4.plot(t, Z, "m")
ax5 = fig2.add_subplot(224)
ax5.plot(Y, Z, "r")

fig1 enthält nur einen Subplot (111) (die Ziffern bezeichnen die Anzahl der Reihen, der Spalten und die fortlaufende Nummer des Plots), 111 bedeutet daher, daß das Fenster nur eine Reihe, eine Spalte und folglich auch nur einen (Sub-) Plot enthält.

fig2 dagegen bekommt zwei Reihen, zwei Spalten und damit vier Subplots zugewiesen.

Der Rest ist wie gehabt. Die Lorenzgleichungen habe ich mit dem schon bewährten odeint aus scipy.integrate numerisch lösen lassen. Dadurch ist das Skript von erstaunlicher Kürze:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.integrate import odeint

# Parameter
sigma = 10.0
beta = 8/3.0
rho = 28.0

# Die Lorenzgleichung
def lorenz(u, t, sigma, beta, rho):
    x, y, z = u
    dxdt = sigma*(y - x)
    dydt = rho*x - y - x*z
    dzdt = x*y - beta*z
    return(dxdt, dydt, dzdt)

# Startwerte und Initialisierung
y0 = 5.0, 5.0, 5.0
t = np.linspace(0, 20, 2000)

solution = odeint(lorenz, y0, t, args = (sigma, beta, rho))

X, Y, Z = solution[:,0], solution[:,1], solution[:,2]

fig1 = plt.figure()
ax1 = fig1.add_subplot(111, projection = "3d", title = "Lorenz-Attraktor")
ax1.plot(X, Y, Z, "r")

fig2 = plt.figure()
ax2 = fig2.add_subplot(221)
ax2.plot(t, X, "b")
ax3 = fig2.add_subplot(222)
ax3.plot(t, Y, "c")
ax4 = fig2.add_subplot(223)
ax4.plot(t, Z, "m")
ax5 = fig2.add_subplot(224)
ax5.plot(Y, Z, "r")
plt.show()

Die Matplotlib scheint tatsächlich erstaunlich vielseitig zu sein – auch ohne ein Jupyter-Notebook bemühen zu müssen. Ich werde daher in den nächsten Tagen noch ein paar weitere Experimente damit durchführen. Still digging!

Literatur:

Für die Erkundung des Lorenz-Attraktors sind folgende Quellen sehr hilfreich:

• James Gleick: Chaos – die Ordnung im Universum, München (Knaur) 1990
• Dietmar Herrman: Algorithmen für Chaos und Fraktale, Bonn (Addison-Wesley) 1994
• Ian Stewart: Spielt Gott Roulette?, Frankfurt am Main und Leipzig (Insel) 1993

Bei der Erkundung der Matplotlib hat mir dieses Buch geholfen:

• Sandro Tosi: Matplotlib for Python Developers, Birmingham – Mumbai (Packt) 2009

(Kommentieren)