Das Feigenbaum-Diagramm (ohne (Jupyter-) Notebook)

Erinnert Ihr Euch an Joel Grus’ wunderbaren Rant »I don’t like Notebooks«, den ich am 28. August 2018 hier im Blog Kritzelheft vorgestellt hatte? Seine Arbeitsweise ist meiner ähnlich: Ich schreibe in einem Markdown-Editor (bevorzugt MacDown) und kopiere die Codeschnipsel an passender Stelle hinein. Wie das aussehen kann, möchte ich am Beispiel der logistischen Gleichung (aka Feigenbaum-Diagramm) zeigen:

Das Feigenbaum Diagramm

Die logistische Gleichung wurde ursprünglich 1837 von Pierre François Verhulst als demographisches mathematisches Modell eingeführt. Die Gleichung ist ein Beispiel dafür, wie komplexes, chaotisches Verhalten aus einfachen nichtlinearen Gleichungen entstehen kann. Das möchte ich exemplarisch in Python zeigen:

Zuerst importiere ich die benötigten Pakete Numpy und die Matplotlib:

import numpy as np
import matplotlib.pyplot as plt

Danach implementiere ich die logistische Funktion $x_{n+1} = rx_{n}(1-x_{n})$:

def logistic(r, x):
    return r*x*(1-x)

Zur Berechnung der Funktion wird ein Array mit 10.000 Werten implementiert, die zwischen 2,5 und 4 gleichverteilt sind:

n = 10000
r = np.linspace(2.5, 4.0, n)

Das Programm soll 1.000 Iterationen der logistischen Gleichung durchlaufen und die letzten 100 sollen für das Bifurkations-Diagramm genutzt werden.

iterations = 1000
last = 100

Das System wird mit $x_{0} = 0.0001$ initialisiert:

x = 1e-5 * np.ones(n)

Zur Berechnung des Lyanpunov-Exponenten (ich weiß, die Wikipedia schreibt »Ljapunow«, aber damit steht sie ziemlich allein auf weiter Flur) wird nun noch der lyapunov-Vektor initialisiert:

lyapunov = np.zeros(n)

Mit ggplot (gg steht für Grammar of Graphics) wird der Plot noch ein wenig aufgehübscht:

plt.style.use("ggplot")
plt.subplots_adjust(hspace = 0.6)

Und nun wird berechnet und gezeichnet:

plt.subplot(211)
for i in range(iterations):
    x = logistic(r, x)
    lyapunov += np.log(abs(r - 2*r*x))
    if i >= (iterations - last):
        plt.plot(r, x, ",k", alpha = 0.02)
plt.xlim(2.5, 4.0)
plt.title("Feigenbaum-Diagramm")

plt.subplot(212)
plt.plot(r[lyapunov < 0], lyapunov[lyapunov < 0]/iterations, ",k", alpha = 0.1)
plt.plot(r[lyapunov >= 0], lyapunov[lyapunov >= 0]/iterations, ",r", alpha = 0.25)
plt.xlim(2.5, 4.0)
plt.ylim(-2, 1)
plt.title("Lyapunov-Exponent")

plt.show()

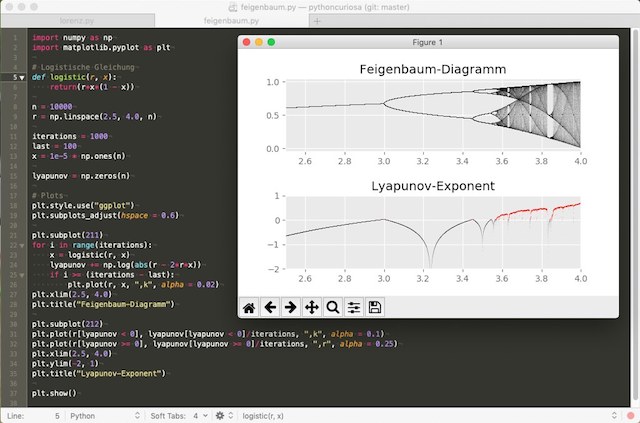
Das Ergebnis kann sich sehen lassen:

Es gibt einen Fixpunkt und die erste Bifurkation bei $r = 3.0$ und der Lyapunov-Exponent ist positiv (hier in rot markiert), wenn das System chaotisch wird. Bei jeder Nullstelle des Exponenten finden weitere Bifurkationen statt.

Caveat: Ich habe es in diesem Beispiel mit der Notebook-Ähnlichkeit ein wenig übertrieben, das Meiste hätte ich auch mit simplen Kommentaren im Quelltext erledigen können, aber ich wollte einfach zeigen, daß man auch ohne Jupyter-Notebook notebookähnliche Tutorials verfassen kann.

1 (Email-) Kommentar

Du hättest vielleicht noch erwähnen können (im Sinne des verbesserten click bait), dass die logistische Differentialgleichung eingesetzt werden kann, um näherungsweise den Verlauf einer Pandemie zu beschreiben.

– Alexander A. (Kommentieren) (#)

(Kommentieren)