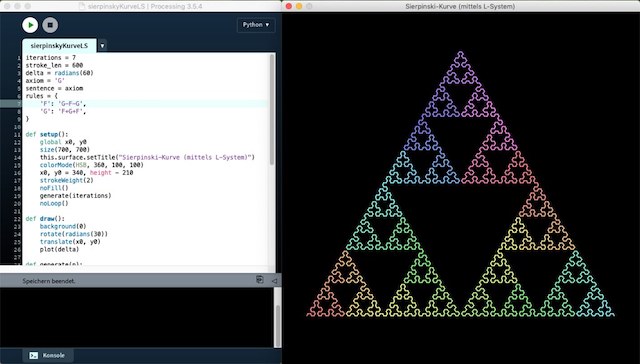
Spaß mit Processing.py: Das Sierpinski-Dreieck als L-System

Eine Lindenmayer- oder L-System – entwickelt von dem ungarischen theoretischen Biologen Aristid Lindenmayer – ist eine auf Noam Chomskys Arbeiten zu fromalen Grammatiken beruhende formale Sprache, die Lindenmayer 1968 als Grundlage einer axiomatischen Theorie biologischer Entwicklung entwarf. Die L-Systeme werden sowohl in der Computergraphik bei der Erzeugung von Fraktalen wie auch in der realitätsnahen Modellierung von Pflanzen genutzt.

Ein kontextfreies L-System (0L-System) besteht aus einem Axiom und einer endlichen Anzahl von Produktionsregeln. Um zum Beispiel eine Ikone der fraktalen Geometrie, das Sierpinki-Dreieck (Sierpinski-Kurve) mit einem L-System zu erzeugen, benötigt man ein Axion G und die Produktionsregeln oder Ersetzungsregeln:

    'F': 'G-F-G',
    'G': 'F+G+F',

Bei jeder Iteration wird nun jedes F durch G-F-G und jedes G durch F+G+F ersetzt. Dabei können F und G als Zeichnen einer Strecke und - und + als Links- respektive als Rechtsdrehung interpretiert werden. Der Drehwinkel delta wird im Programm vorgegeben.

Im Programm wird die vollständige Zeichenkette des L-Systems zur Erzeugung des Sierpinksi-Dreiecks in der Funktion generate() erzeugt und das Dreieck wird mit der Funktion plot() gezeichnet:

iterations = 7
stroke_len = 600
delta = radians(60)
axiom = 'G'
sentence = axiom
rules = {
    'F': 'G-F-G',
    'G': 'F+G+F',
}

def setup():
    global x0, y0
    size(700, 700)
    this.surface.setTitle("Sierpinski-Kurve (mittels L-System)")
    colorMode(HSB, 360, 100, 100)
    x0, y0 = 340, height - 210
    strokeWeight(2)
    noFill()
    generate(iterations)
    noLoop()
 
def draw():
    background(0)
    rotate(radians(30))
    translate(x0, y0)
    plot(delta)
 
def generate(n):
    global stroke_len, sentence
    for i in range(n):
        stroke_len *= 0.5
        next_sentence = ''
        for c in sentence:
            next_sentence += rules.get(c, c)
        sentence = next_sentence

def plot(angle):
    k = 0
    for c in sentence:
        if c == 'F' or c == 'G':
            stroke(int(k%360), 50, 100)
            line(0, 0, 0, -stroke_len)
            translate(0, -stroke_len)
            k += 0.25
        elif c == '+':
            rotate(angle)
        elif c == '-':
            rotate(-angle)

Um das alles mit ein wenig Farbe aufzuhübschen, habe ich den HSB-Farbraum gewählt, da man dort anschaulicher den Farbkreis durchwandern kann.

Die Aufteilung des Programms in setup() und draw() ist rein artifiziell, da durch noLoop() keine wiederholten Durchläufe stattfinden. Man hätte also auch auf die Aufteilung in setup() und draw() verzichten und alles in einem Durchlauf sequentiell abarbeiten können. Ich finde aber, daß die Aufteilung in einzelne Funktionen den Sketch übersichtlicher gestaltet.

Das L-System für das Sierpinski-Dreieck habe ich Dieter Hermanns Buch Algorithmen für Chaos und Fraktale, Bonn (Addison Wesley) 1994, Seite 203 entnommen und der Processing.py-Sketch wurde durch einen ähnlichen Sketch von Rosetta Code inspiriert.

(Kommentieren)