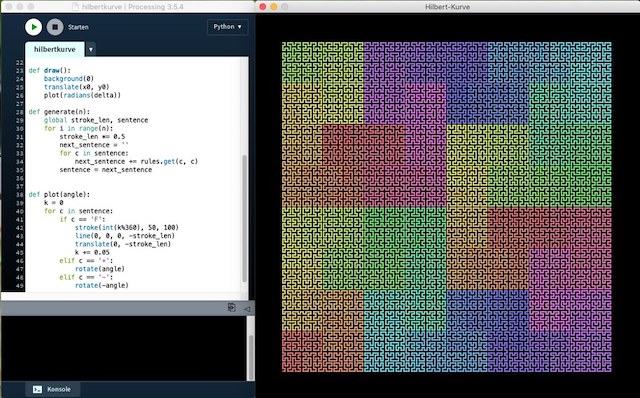
Noch mehr Spaß mit Processing.py: Die Hilbert-Kurve als L-System
Wenn ich schon einmal mit L-Systemen angefangen hatte, wollte ich auch gleich eine andere Ikone der fraktalen Geometrie als L-System in Processing.py implementieren: Die Hilbert-Kurve wurde 1891 von dem deutschen Mathematiker David Hilbert entdeckt. Sie ist eine stetige Kurve, die als Grenzkurve von Polygonzügen die Fläche eines Quadrats vollständig ausfüllt. Sie ist daher eine raumfüllende Kurve. Die Möglichkeit, mit einer stetigen eindimensionalen Kurve ein zweidimensionales Gebiet komplett abdecken zu können, war den Mathematikern des neunzehnten Jahrhunderts neu, solche Kurven wurde deshalb auch als Monsterkurven bezeichnet. Die meisten Monsterkurven – so auch die Hilbert-Kurve – sind Fraktale.
Der Sketch ist weitestgehend mit dem Sketch zum Sierpinski-Dreieck identisch und hier wie dort habe ich auch die Produktionsregeln aus Dieter Hermanns Buch Algorithmen für Chaos und Fraktale, Bonn (Addison Wesley) 1994, Seite 205 entnommen.
iterations = 7 stroke_len = 600 delta = 90 axiom = 'X' sentence = axiom rules = { 'X': '+YF-XFX-FY+', 'Y': '-XF+YFY+FX-', } i = 0 def setup(): global x0, y0 size(700, 700) this.surface.setTitle("Hilbert-Kurve") colorMode(HSB, 360, 100, 100) x0, y0 = 50, height - 50 strokeWeight(2) noFill() generate(iterations) noLoop() def draw(): background(0) translate(x0, y0) plot(radians(delta)) def generate(n): global stroke_len, sentence for i in range(n): stroke_len *= 0.5 next_sentence = '' for c in sentence: next_sentence += rules.get(c, c) sentence = next_sentence def plot(angle): k = 0 for c in sentence: if c == 'F': stroke(int(k%360), 50, 100) line(0, 0, 0, -stroke_len) translate(0, -stroke_len) k += 0.05 elif c == '+': rotate(angle) elif c == '-': rotate(-angle)
Über …
Der Schockwellenreiter ist seit dem 24. April 2000 das Weblog digitale Kritzelheft von Jörg Kantel (Neuköllner, EDV-Leiter Rentner, Autor, Netzaktivist und Hundesportler — Reihenfolge rein zufällig). Hier steht, was mir gefällt. Wem es nicht gefällt, der braucht ja nicht mitzulesen. Wer aber mitliest, ist herzlich willkommen und eingeladen, mitzudiskutieren!
Alle eigenen Inhalte des Schockwellenreiters stehen unter einer Creative-Commons-Lizenz, jedoch können fremde Inhalte (speziell Videos, Photos und sonstige Bilder) unter einer anderen Lizenz stehen.
Der Besuch dieser Webseite wird aktuell von der Piwik Webanalyse erfaßt. Hier können Sie der Erfassung widersprechen.
Diese Seite verwendet keine Cookies. Warum auch? Was allerdings die iframes von Amazon, YouTube und Co. machen, entzieht sich meiner Kenntnis.
Werbung
Diese Spalte wurde absichtlich leergelassen!