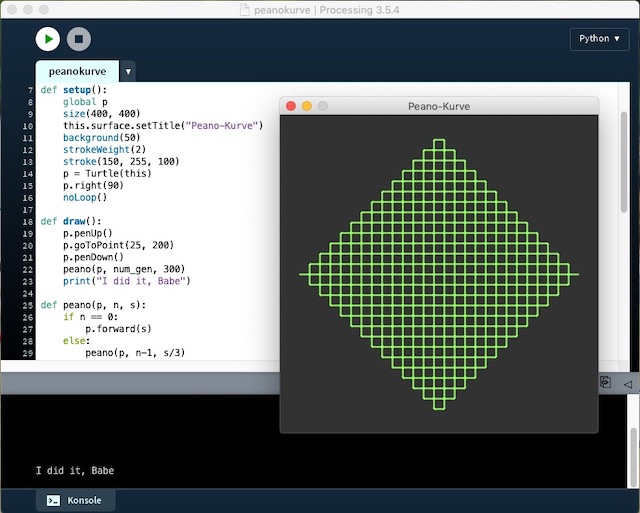
Noch mehr Spaß mit der Turtle in Processing.py: Die Peano-Kurve

Weil es so viel Spaß bereitet hat und weil es so einfach war, habe ich gleich noch eine zweite flächenfüllende Kurve mit der Schildkröte in Processing.py implementiert: Die Peano-Kurve, benannt nach dem Mathematiker Giuseppe Peano¹. Auch sie besitzt als raumfüllende Kurve die Haussdorf-Dimension 2 und entspricht in ihrer Struktur Cantors erstem Diagonalargument (das heißt, die Kurve ist in ihrem Grenzwert »abzählbar unendlich«).

Doch das soll hier nicht zu einer Mathematik-Stunde ausarten (obwohl Mathematik natürlich Spaß macht), daher ganz schnell den Quellcode, der sich im Prinzip nur in der Funktion peano() von dem der Drachenkurve unterscheidet:

add_library('Turtle')
import math

num_gen = 3
ds = 1

def setup():
    global p
    size(400, 400)
    this.surface.setTitle("Peano-Kurve")
    background(50)
    strokeWeight(2)
    stroke(150, 255, 100)
    p = Turtle(this)
    p.right(90)
    noLoop()

def draw():
    p.penUp()
    p.goToPoint(25, 200)
    p.penDown()
    peano(p, num_gen, 300)
    print("I did it, Babe")
    
def peano(p, n, s):
    if n == 0:
        p.forward(s)
    else:
        peano(p, n-1, s/3)
        p.left(45)
        p.forward(ds*math.sqrt(2))
        p.left(45)
        peano(p, n-1, s/3)
        p.right(45)
        p.forward(ds*math.sqrt(2))
        p.right(45)
        peano(p, n-1, s/3)
        p.right(45)
        p.forward(ds*math.sqrt(2))
        p.right(45)
        peano(p, n-1, s/3)
        p.right(45)
        p.forward(ds*math.sqrt(2))
        p.right(45)
        peano(p, n-1, s/3)
        p.left(45)
        p.forward(ds*math.sqrt(2))
        p.left(45)
        peano(p, n-1, s/3)
        p.left(45)
        p.forward(ds*math.sqrt(2))
        p.left(45)
        peano(p, n-1, s/3)
        p.left(45)
        p.forward(ds*math.sqrt(2))
        p.left(45)
        peano(p, n-1, s/3)
        p.right(45)
        p.forward(ds*math.sqrt(2))
        p.right(45)
        peano(p, n-1, s/3)

Da diese Peano-Kurve so konstruiert ist, daß über dem Generator – einer geraden Linie – im zweiten Drittel je in der Seitenlänge gedritteltes Quadrate über und unter der Linie gezeichnet werden, hat die Schildkröte ganz gut zu tun und darum ist die Funktion peano() auch etwas lang geraten. Und die Zeile ds = 1 scheint etwas seltsam, da Eins multipliziert mit Irgendetwas immer nur Irgendetwas ergibt, also nichts am Wert von Irgendetwas ändert. Sie macht aber dennoch Sinn, denn wenn man weitere Generationen der Kurve zeichnen lassen möchte und die Kurve noch in das Ausgabefenster passen soll, muß der Wert von ds verringert werden. So sollte man bei num_gen = 4 den Wert ds = 0.75 einsetzen und bei num_gen = 5 sogar ds = 0.25. Die fünfte Generation unterscheidet sich kaum noch von einem vollständig gefüllten Karo und man muß schon einige Sekunden auf die Ausgabe im Zeichenfenster warten.

(Kommentieren)