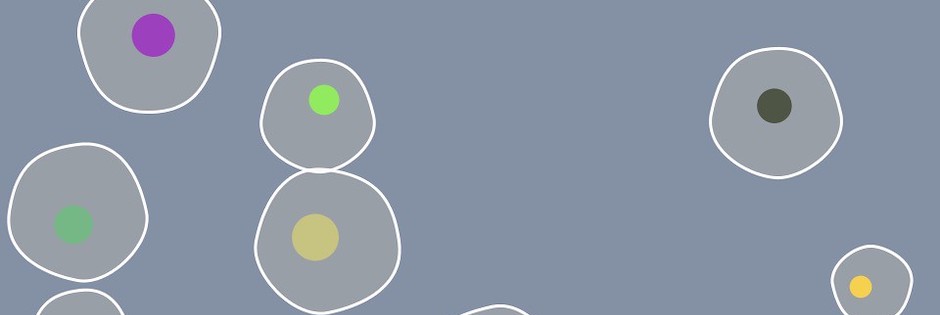
Amöben in der Petrischale (Simulation mit Processing.py)
Ich bin Euch noch die Berichte meiner letzten Experimente mit Processing.py schuldig. Am vorletzten Sonntag hatte ich – inspiriert von einem Kapitel aus »Learn Python Visually« von Tristan Bunn – eine Art Simulation von Amöben in einer Petrischale programmiert. Natürlich ist es keine echte Simulation, selbst so einfache Einzeller wie Amöben zeigen doch ein deutlich komplexeres Verhalten. Es ist eher eine Variante meines Bubble Busters von vor vierzehn Tagen, nur bedeutend rechenintensiver.
Daß diese »Simulation« soviel Rechenleistung verbraucht, liegt an der Darstellung der Membrane der Amöbe. Während der Kern einfach nur ein (farbiger) Kreis ist, der zufällig versetzt von einem gedachten Mittelpunkt des Einzellers plaziert wird, wabert die Membrane um den Kern herum. Dies wird mit Hilfe von Bezier-Kurven und einer Darstellung in Polarkoordinaten (Methode circle_point()) realisiert und das sieht im Quelltext folgendermaßen aus:
def show(self):
# nucleus
fill(self.nucleus["fill"])
noStroke()
circle(self.location.x + self.nucleus["x"], self.location.y + self.nucleus["y"],
self.nucleus["d"])
# cell membrane
fill(234, 218, 184, 50)
stroke(255, 255, 255)
strokeWeight(3)
r = self.d/2.0
cpl = r*0.55
cpx, cpy = self.circle_point(2*frameCount/(r/2), r/8)
xp, xm = self.location.x + cpx, self.location.x - cpx
yp, ym = self.location.y + cpy, self.location.y - cpy
with beginShape():
vertex(self.location.x, self.location.y - r) # top vertex
bezierVertex(xp + cpl, yp - r, xm + r, ym - cpl,
self.location.x + r, self.location.y) # right vertex
bezierVertex(xp + r, yp + cpl, xm + cpl, ym + r,
self.location.x, self.location.y + r) # bottom vertex
bezierVertex(xp - cpl, yp + r, xm - r, ym + cpl,
self.location.x - r, self.location.y) # left vertex
bezierVertex(xp - r, yp - cpl, xm - cpl, ym - r,
self.location.x, self.location.y - r) # back to top vertex
def circle_point(self, theta, rho):
x = cos(theta)*rho
y = sin(theta)*rho
return[x, y]
Bei einer Wiederholung von 60 Frames in der Sekunde gerät mein betagtes MacBook Pro schon gnz schön ins Schwitzen und mußte wiederholt den Lüfter anwerfen.
Doch hier erst einmal der restliche Quellcode der Klasse Amoeba:
class Amoeba():
def __init__(self, _x, _y, _diameter, _x_speed, _y_speed):
self.location = PVector(_x, _y)
self.propulsion = PVector(_x_speed, _y_speed)
self.d = _diameter
self.nucleus = {
"fill": color(random(20, 250), random(20, 250), random(20, 250)),
"x": self.d*random(-0.15, 0.15),
"y": self.d*random(-0.15, 0.15),
"d": self.d/random(2.5, 4)
}
def update(self):
self.location += self.propulsion
r = self.d/2
if (self.location.x + r > width) or (self.location.x - r < 0):
self.propulsion.x *= -1
if (self.location.y + r > height) or (self.location.y - r < 0):
self.propulsion.y *= -1
Er folgt der üblichen Reihenfolge Konstruktor (__init__()), und dann den Methoden update() und show() (mit der Hilfsmethode circel_point()).
Die Kollisionserkennung habe ich dieses Mal nicht in der Klasse Amoeba implementiert, sondern sie in Hauptprogramm verschoben, das wie folgt ausieht:
from amoeba import Amoeba
WIDTH = 960
HEIGHT = 540
FPS = 60
counter = 0
amoebas = []
for i in range(8):
diameter = random(50, 150)
x_speed = 1000/(diameter*(500*random(-2, 2)))
if x_speed == 0:
x_speed = 1000/(diameter*(500))
y_speed = 1000/(diameter*(500*random(-2, 2)))
if y_speed == 0:
y_speed = 1000/(diameter*(500))
radius = diameter/2
x, y = random(radius, WIDTH - radius), random(radius, HEIGHT - radius)
amoebas.append(Amoeba(x, y, diameter, x_speed, y_speed))
def setup():
size(WIDTH, HEIGHT)
this.surface.setTitle(u"Amöben in der Petrischale")
frameRate(FPS)
def draw():
background(132, 144, 163)
for amoeba in amoebas:
amoeba.update()
amoeba.show()
# collision detection
for other in amoebas:
if amoeba is other:
continue
distance = amoeba.location - other.location
sum_radii = amoeba.d/2 + other.d/2
if distance.mag() < sum_radii:
amoeba.propulsion += distance.limit(0.05)
other.propulsion -= distance.limit(0.05)
Natürlich sind Amöben keine Seifenblasen, die zerplatzen, wenn sie kollidieren, sondern sie werden jeweils in entgegengesetzte Richtungen voneinander abgestoßen. Das passiert in diesen Zeilen:
if distance.mag() < sum_radii:
amoeba.propulsion += distance.limit(0.05)
other.propulsion -= distance.limit(0.05)
Durch das Wabern der Zellmembranen stellen diese nur annähernd Kreise dar. Dadurch überlappen sich gelegentlich die Amöben bei einer Kollision ein wenig. In diesem Video kann man dies beobachten:
Den Quellcode gibt es wie immer auch auf GitHub. Viel Spaß mit der kleinen Amöbenpopulation. Wer einen etwas »fetteren« Rechner hat, kann es ja auch mal mit einer größeren Population versuchen.
Über …
Der Schockwellenreiter ist seit dem 24. April 2000 das Weblog digitale Kritzelheft von Jörg Kantel (Neuköllner, EDV-Leiter Rentner, Autor, Netzaktivist und Hundesportler — Reihenfolge rein zufällig). Hier steht, was mir gefällt. Wem es nicht gefällt, der braucht ja nicht mitzulesen. Wer aber mitliest, ist herzlich willkommen und eingeladen, mitzudiskutieren!
Alle eigenen Inhalte des Schockwellenreiters stehen unter einer Creative-Commons-Lizenz, jedoch können fremde Inhalte (speziell Videos, Photos und sonstige Bilder) unter einer anderen Lizenz stehen.
Der Besuch dieser Webseite wird aktuell von der Piwik Webanalyse erfaßt. Hier können Sie der Erfassung widersprechen.
Diese Seite verwendet keine Cookies. Warum auch? Was allerdings die iframes von Amazon, YouTube und Co. machen, entzieht sich meiner Kenntnis.
Werbung
Diese Spalte wurde absichtlich leergelassen!