Auf der Suche nach der Mona Lisa in der Kreiszahl Pi

Das »Theorem der endlos tippenden Affen« besagt, daß man, wenn man eine Horde Affen vor Schreibmaschinen setzt und sie zufällig darauf herumtippen, dabei irgendwann einmal – neben vielem Unsinn – die Werke William Shakespeares und/oder alle Bücher der Berliner Staatsbibliothek herauskommenen müssen. Das Theorem ist formal bewiesen und daran ist nichts zu deuteln. Numberphile geht in diesem Video noch einen Schritt weiter und fragt: Wenn man die (unendlichen) Nachkommastellen der Kreiszahl Pi in geeigneter Form visualisiert, müßte dann nicht irgendwann einmal ein Abbild der Mona Lisa herauskommen?

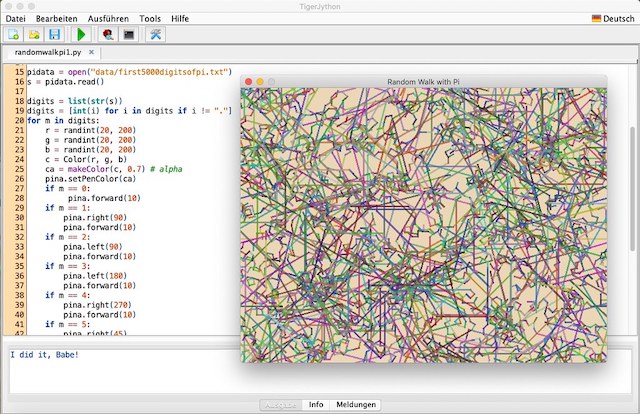
Als »geeignetes« Visualisierungsverfahren haben sie in dem Video einen Random Walk herausgesucht. Das hat mich natürlich elektrisiert, weil es gut in meine derzeitigen Experimente mit TigerJython paßt. Also habe ich solch ein Verfahren auch einmal implementiert. Dabei habe ich ganz einfache Annahmen getroffen: Die Schrittweite der Turtle bei jeder Nachkommastelle beträgt \(10\), außer bei der \(6\), da beträgt die Schrittweite \(100\).

Die jeweiligen Winkel sind: Bei der \(0\) 0°, bei der \(1\) 90° rigth, der \(2\) 90° left, der \(3\) 180° left, der \(4\) 270° right, der \(5\) 45° right, der \(6\) 45° left, der \(7\) 60° right, der \(8\) 60° left und schließlich bei der \(9\) sind es 30° left. Die Werte sind rein artifiziell und Ihr seid aufgefordert, mit anderen Werten zu experimentieren.

Gegossen habe ich das Experiment in diese wenigen Zeilen Python-Code. Dabei habe ich mich bei der Farbauswahl an meinem bisherigen Experimenten mit TigerJython und dem Random Walker orientiert:

from gturtle import *
from random import randint

WIDTH, HEIGHT = 640, 480

setPlaygroundSize(WIDTH, HEIGHT)
playground = TurtleFrame()
playground.title = "Random Walk with Pi"
playground.clean(Color(235, 215, 182)) # Packpapier

pina = Turtle(playground)
pina.hideTurtle()
pina.setLineWidth(3)

pidata = open("data/first5000digitsofpi.txt")
s = pidata.read()

digits = list(str(s))
digits = [int(i) for i in digits if i != "."]
for m in digits:
    r = randint(20, 200)
    g = randint(20, 200)
    b = randint(20, 200)
    c = Color(r, g, b)
    ca = makeColor(c, 0.7) # alpha
    pina.setPenColor(ca)
    if m == 0:
         pina.forward(10)
    if m == 1:
        pina.right(90)
        pina.forward(10)
    if m == 2:
        pina.left(90)
        pina.forward(10)
    if m == 3:
        pina.left(180)
        pina.forward(10)
    if m == 4:
        pina.right(270)
        pina.forward(10)
    if m == 5:
        pina.right(45)
        pina.forward(10)
    if m == 6:
        pina.left(45)
        pina.forward(100)
    if m == 7:
        pina.right(60)
        pina.forward(10)
    if m == 8:
        pina.left(60)
        pina.forward(10)
    if m == 9:
        pina.left(30)
        pina.forward(10)
    
    pina.wrap()

print("I did it, Babe!")

De Zahlen für die Nachkommastellen von Pi habe ich auf dieser Seite berechnen lassen und für 5.000 Stellen in der Datei first5000digitsofpi.txt und für 10.000 Stellen in first10000digitsofpi.txt im Unterverzeichnis data abgelegt. Für besonders Experimentierfreudige habe ich dort auch noch die Datei onemilliondigitsofpi.txt von dieser Seite abgelegt, aber glaubt mir, die Millionen bringen keinen weiteren Erkenntnisgewinn, das ergibt nur einen völlig zu- und überschriebenen Bildschirm. Da müßten andere Formen der Visualisierung gefunden werden.

Die Macher der Numberphile haben auch in den ersten Millionen Stellen keine Mona Lisa gefunden, das Bannerbild oben ist ein Fake. Aber das bedeutet nicht, daß sich die Mona Lisa nicht noch tiefer in den Nachkommastellen verbirgt, denn was sind schon eine millionen Dezimalstellen? Das ist ein Nichts, ein Fliegenschiß im Meer der Unendlichkeit.

Dann ist auch noch umstritten, ob das Affentheorem überhaupt auf die Nachkommastellen von Pi anwendbar ist. Zwar spricht vieles dafür, daß die Dezimalstellen von Pi eine gute Quelle für (Pseudo-) Zufallszahlen sind, aber bewiesen ist die Normalität der Kreiszahl bis heute nicht.

Mit der Schildkröte und Pi lassen sich noch einige hübsche Visualisierungen produzieren. Numberphile stellt ein paar davon in dem Video vor. Ich werde sicher in späteren Beiträgen darauf zurückkommen. Still digging!

Den Quellcode wie auch die Dateen mit den Nachkommastellen von Pi könnt Ihr in meinem GitLab-Repositorium zu TigerJython finden.

(Kommentieren)