Thinking about Refactoring »The Nature of Code« (with Py5?)

Als ich heute vormittag mit meinem Chromebook auf unserer Terrasse saß und mich freute, daß ich dort mit Python, Py5 und Thonny spielen konnte, kam mir der verwegene Gedanke, daß ich ja Daniel Shiffmans in Processing implementiertes, wunderbares Buch »The Nature of Code« nach Py5 portieren könnte. Der Gedanke mag zwar verwegen sein, wirklich neu ist er nicht. Denn seit 2018 versucht Shiffman die Zeit zu finden, eine Neuinterpretation dieses Buches nach P5.js zu schreiben und inspiriert davon und parallel dazu habe ich mich auch schon an diversen Python-Ports versucht (zum Beispiel nach Processing.py, der Python Arcade-Bibliothek, Pygame Zero oder TigerJython).

Wieso kocht also das Thema bei mir wieder hoch? Weil ich mich ein wenig durch die Dokumentation zu Py5 gewühlt und dort festgestellt hatte, daß Py5 eine auf Numpy basierende Implementierung einer Vektorklasse besitzt. Und »The Nature of Code« behandelt im Kern das Programmieren mit Vektoren. Und weil ich in den letzten Wochen ein wenig mit Numerik gespielt hatte und dabei zu der Überzeugung gelangt war, daß jeder Programmierer auch mal numerische Algorithmen »von Hand« implementieren sollte, statt sich auf fertige Bibliotheken zu verlassen. Bei diesen Überlegungen hat mich Veit Steinkamp mit seinen Büchern »Mathematische Algorithmen mit Python« und »Der Python-Kurs für Ingenieure und Naturwissenschaftler« unterstützt, die ich Euch wärmstens ans Herz legen kann.

Das zusammen schreit geradezu nach einer Neuinterpretation von »The Nature of Code«. Vor allem da Shiffman in seinem Buch an vielen Stellen die mathematischen und physikalischen Gesetze stark vereinfacht. Das ist nicht wirklich falsch und für seine Zielgruppe (Künstler und andere Kreative) in der Regel okay, aber manches mal hätte ich mir bei der Lektüre doch gewünscht, daß Shiffmans Lösungen näher an der physikalischen Wirklichkeit lägen. Und da kommt nun Py5 ins Spiel. Py5 spielt mit Numpy, SciPy und den anderen Python-3-Paketen aus dem naturwissenschaftlichen Stack zusammen und ist daher prädestiniert für solche Probleme und ihre naturwissenschaftlichen Lösungen – zumindest hoffe ich das.

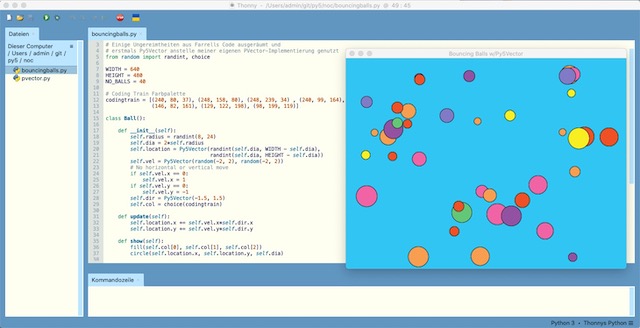
Als erste Fingerübung habe ich mal das bewährte Bouncing Balls Beispiel in Py5 mit Py5-Vektor implementiert. Meine Lösung sieht so aus:

# Bouncing Balls w/ Classes (improved)
# nach Peter Farrell »Math Adventures with Python«, p183ff
# Einige Ungereimtheiten aus Farrells Code ausgeräumt und
# erstmals Py5Vector anstelle meiner eigenen PVector-Implementierung genutzt
from random import randint, choice

WIDTH = 640
HEIGHT = 480
NO_BALLS = 40

# Coding Train Farbpalette
codingtrain = [(240, 80, 37), (248, 158, 80), (248, 239, 34) , (240, 99, 164),
               (146, 82, 161), (129, 122, 198), (98, 199, 119)]

class Ball():
    
    def __init__(self):
        self.radius = randint(8, 24)
        self.dia = 2*self.radius
        self.location = Py5Vector(randint(self.dia, WIDTH - self.dia),
                                  randint(self.dia, HEIGHT - self.dia))
        self.vel = Py5Vector(random(-2, 2), random(-2, 2))
        # No horizontal or vertical move
        if self.vel.x == 0:
            self.vel.x = 1
        if self.vel.y == 0:
            self.vel.y = -1
        self.dir = Py5Vector(-1.5, 1.5)
        self.col = choice(codingtrain)
        
    def update(self):
        self.location.x += self.vel.x*self.dir.x
        self.location.y += self.vel.y*self.dir.y
    
    def show(self):
        fill(self.col[0], self.col[1], self.col[2])
        circle(self.location.x, self.location.y, self.dia)
    
    def check_boundaries(self):
        if self.location.x > width - self.radius or self.location.x < self.radius:
            self.vel.x *= -1
        if self.location.y > height - self.radius or self.location.y < self.radius:
            self.vel.y *= -1            
balls = []       

def setup():
    size(WIDTH, HEIGHT)
    window_move(1400, 30)
    window_title("Bouncing Balls w/Py5Vector")
    for _ in range(NO_BALLS):
        balls.append(Ball())

def draw():
    background(49, 197, 244)   # Hellblau
    for ball in balls:
        ball.show()
        ball.check_boundaries()
        ball.update()

Das Skript unterscheidet sich noch nicht großartig von meiner eigenen PVector-Implementierung, aber es ist der Beweis dafür, daß Py5 und Numpy zusammenspielen. Daraus müßte sich doch etwas machen lassen. Still digging!

(Kommentieren)