Spaß mit Processing.py: Re-Enactment und Re-Mixing

Mit diesem Aufsatz hatte mich Stefan Höltgen inspiriert, auch einmal ein paar frühe Exemplare der Computerkunst nachzuprogrammieren. Bei meinen Re-Enactment-Versuchen wollte ich aber durchaus eine »moderne« Programmiersprache einsetzen (Processing.py, den Python-Mode von Processing), denn ich glaube, daß durch den Einsatz einer »historischen« Sprache (Höltgen nutzte BBC-BASIC, ein BASIC-Dialekt aus dem Jahre 1981) kein wirklicher Erkenntnis-Gewinn erfolgen kann. Das leite ich schon alleine aus der Tatsache ab, daß die besprochenen und nachprogrammierten Werke in den 1960er und frühen 1970er Jahren entstanden waren und vermutlich durch die Bank in ALGOL 60 und/oder FORTRAN (FORTRAN IV, FORTRAN 66) programmiert wurden. Zwar kann man FORTRAN unter Vorbehalt druchaus als »Vorgänger« von BASIC bezeichnen, die ALGOL-Sprachfamilie mündete aber durch die Beteiligung von Niklaus Wirth an Algol W in Pascal und deren Nachfolger¹.

Meine Motivation, diese alten Klassiker nachzuprogrammieren oder als Remix neu zu interpretieren entspricht daher eher dem, was John Nelson Rose unter Retro Games as a Revivalist Movement beschrieben hat. Er vergleicht dort das heutige Revival der Computerspiele der 1980er Jahre mit dem Neoklassizismus und der Neugotik des 19. Jahrhunderts in der Architektur. Beide waren von einer nostalgischen Sehnsucht nach der Vergangenheit geleitet, nutzten aber eigentlich nur die Formensprache, ohne auf moderne Werkzeuge und Erungenschaften zu verzichten (auch im 19. Jahrhunder hätte niemand mehr in einem Schloß Babelsberg ohne Wassertoilette wohnen wollen).

A. Michael Noll: »Vertical-Horizontal Number Three« (1965)

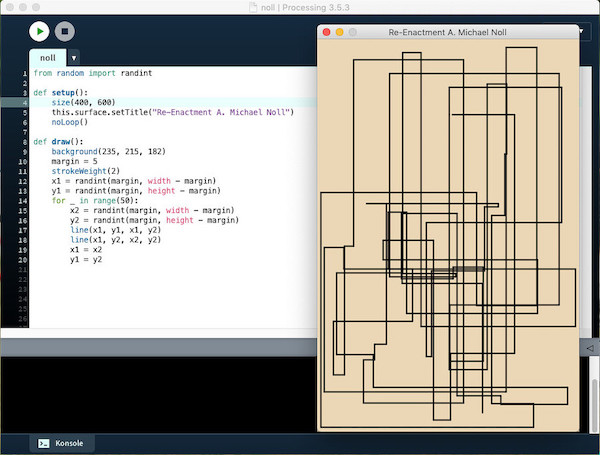
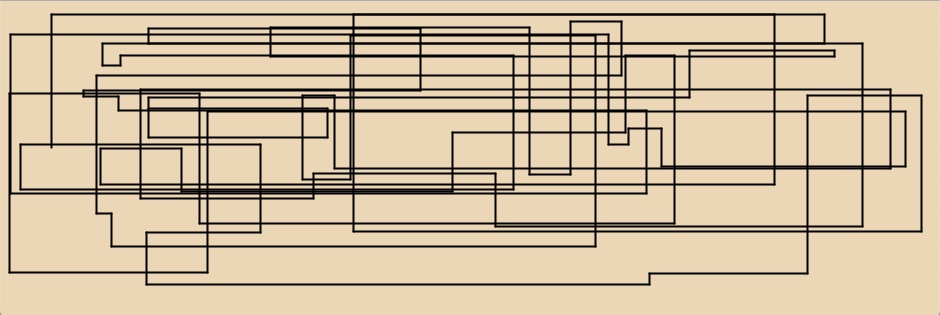
Okay, genug der Vorrede beginnen wir mit einem Werk von A. Michael Noll: »Vertical-Horizontal Number Three« aus dem Jahre 1965. A. Michael Noll programmierte damals ausschließlich in FORTRAN, daher war Höltgens BBC-BASIC-Code hier eine große Hilfe er ersparte mir das Auszählen der senkrechten und waagrechten Linien:

Hier kommt natürlich dem (Nach-) Programmierer zugute, daß die Processing-IDE (PDE) als Sketchbook ausgelegt ist: Man startet das Programm einfach so oft, bis man eine ansprechende Version des Bildes gefunden hat. Diese kann man dann abspeichern.

Hier der Quelltext des Sketches:

from random import randint

margin = 5

def setup():
    size(400, 600)
    this.surface.setTitle("Re-Enactment A. Michael Noll")
    noLoop()
    
def draw():
    background(235, 215, 182)
    strokeWeight(2)
    x1 = randint(margin, width - margin)
    y1 = randint(margin, height - margin)
    for _ in range(50):
        x2 = randint(margin, width - margin)
        y2 = randint(margin, height - margin)
        line(x1, y1, x1, y2)
        line(x1, y2, x2, y2)
        x1 = x2
        y1 = y2

Ich habe die Dicke des Plotterstiftes (strokeWeight) auf 2 gesetzt und dem Bild einen packpapierfarbenen Hintergrund spendiert (ey, ich mag das einfach).

Herbert W. Franke: Quadrate

Zumindest in Deutschland kann man keine Arbeit über Computerkunst schreiben, ohne nicht auf den SF-Autoren und Computerkünstler Herbert W. Franke einzugehen. Ich folge daher hier ebenfalls Höltgen und programmierte sein 1969-1970 entstandenes Werk »Quadrate« nach. Von dem Bild existieren viele Versionen, allerdings habe ich nicht herausbekommen, welche Programmiersprache Franke damals nutzte. Außerdem firmieren Versionen des Bildes auch unter dem Titel »79 Quadrate«, aber ich hielt selbst die von Höltgen heuristisch ermittelten 204 Quadrate für zu wenig, daher nutzt meine Implementierung 254 Quadrate:

from random import randint

magenta  = color(247, 114, 205)
orange   = color(252, 188, 117)
darkgrey = color(84, 72, 74)

def setup():
    size(400, 600)
    this.surface.setTitle("Re-Enactment Herbert W. Franke")
    rectMode(CENTER)
    noLoop()

def draw():
    background(250, 250, 250)
    strokeWeight(2)
    noFill()
    for _ in range(100):
        margin = 25
        stroke(orange)
        x = randint(margin, width - margin)
        y = randint(4*margin, height - 4*margin)
        rect(x, y, margin, margin)
    for _ in range(150):
        margin = 8
        stroke(magenta)
        x = randint(margin, width - margin)
        y = randint(12*margin, height - 12*margin)
        rect(x, y, margin, margin)
    for _ in range(4):
        margin = 100
        stroke(darkgrey)
        x = randint(margin/2 + 10, width - margin/2 - 10)
        y = randint(margin + 10, height - margin - 10)
        rect(x, y, margin, margin)

Alle Versionen dieses Bildes, die ich gesehen habe, kennen keine überlappenden schwarzen Quadrate. Bei der Programmierung habe ich darauf aber keine Rücksicht genommen, sondern das Programm einfach so lange wiederholt, bis es ein Bild ohne überlappende schwarze Quadrate auswarf. Diese Vorgehensweise hatte Herbert W. Franke sicher nicht genutzt – es wäre eine enorme Zeit- und Papierverschwendung, einem Plotter Dutzende von Bildern zeichnen zu lassen, bis endlich ein Bild nichtüberlappender, schwarzer Quadrate entsteht.

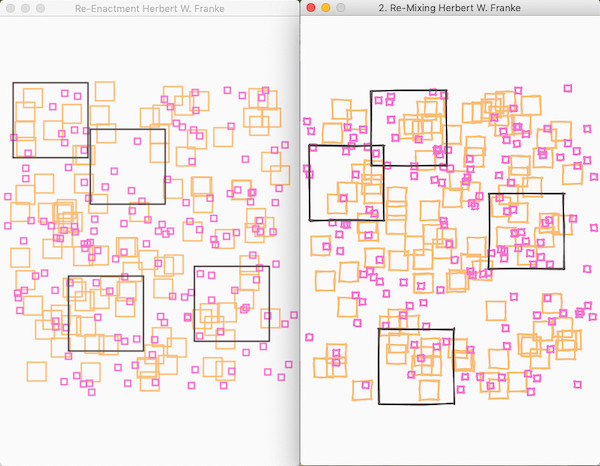
Hier nun mein erstes Remixing: Irgendwie reizte es mich, die strengen, geraden Linien des Plotters wieder aufzubrechen, ihnen eine »humane« Ambiente zurückzugeben. Hierzu habe ich auf die von mir schon mehrfach verwendete und ziemlich geniale Handy Library for Processing zurückgegriffen, die die Ausgabe wie handgezeichnet erscheinen läßt:

add_library('handy')
from random import randint

magenta  = color(247, 114, 205)
orange   = color(252, 188, 117)
darkgrey = color(84, 72, 74)

def setup():
    global h
    size(400, 600)
    this.surface.setTitle("2. Re-Mixing Herbert W. Franke")
    h = HandyRenderer(this)
    rectMode(CENTER)
    h.setRoughness(0.6)
    noLoop()

def draw():
    background(250, 250, 250)
    strokeWeight(2)
    noFill()
    for _ in range(100):
        margin = 25
        stroke(orange)
        x = randint(margin, width - margin)
        y = randint(4*margin, height - 4*margin)
        h.rect(x, y, margin, margin)
    for _ in range(150):
        margin = 8
        stroke(magenta)
        x = randint(margin, width - margin)
        y = randint(12*margin, height - 12*margin)
        h.rect(x, y, margin, margin)
    for _ in range(4):
        margin = 100
        stroke(darkgrey)
        x = randint(margin/2 + 10, width - margin/2 - 10)
        y = randint(margin + 10, height - margin - 10)
        h.rect(x, y, margin, margin)

Wie obiger Screenshot zeigt, war ich auch bei der Überlappung der schwarzen Quadrate nicht mehr so streng. Das Bild gefiel mir und so habe ich es einfach gelassen.

Georg Nees: Schotter (1965)

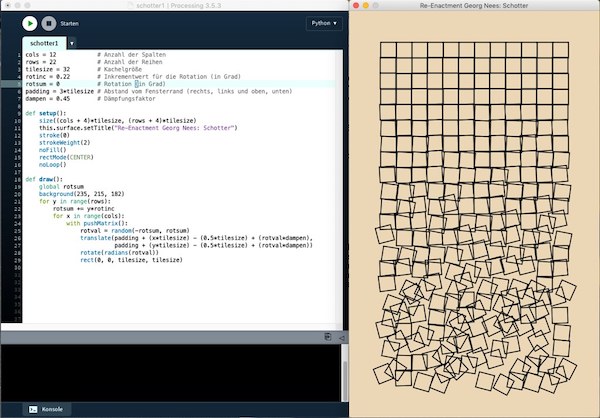
Als letztes Beispiel habe ich mir das Bild »Schotter« von Georg Nees, das dieser etwa 1965 programmiert und geplottet hat vorgenommen. Mein Dank geht mal wieder an Stefan Höltgen, der mich auf eine Processing(Java)-Implementierung von Jim Plaxco hinwies und an Joachim Wedekind, der in seinem wunderbaren Buch »Codierte Kunst« nicht nur »Schotter« in Snap! nachprogrammiert und variiert, sondern auch den Originalcode von Georg Nees veröffentlicht hat. Nees hat seine Version in der »Programmiersprache« G geschrieben, eine DSL, die in der Wirtssprache ALGOL 60 implementiert war². (In Wedekinds Buch gibt es ein ganzes Kapitel zu G – das freut den Wissenschaftshistoriker.)

Das machte eine Reimplementierung in Processing.py natürlich sehr einfach:

cols = 12            # Anzahl der Spalten
rows = 22            # Anzahl der Reihen
tilesize = 32        # Kachelgröße
rotinc = 0.22        # Inkrementwert für die Rotation (in Grad)
rotsum = 0           # Rotation (in Grad)
padding = 3*tilesize # Abstand vom Fensterrand (rechts, links und oben, unten)
dampen = 0.45        # Dämpfungsfaktor

def setup():
    size((cols + 4)*tilesize, (rows + 4)*tilesize)
    this.surface.setTitle("Re-Enactment Georg Nees: Schotter")
    stroke(0)
    strokeWeight(2)
    noFill()
    rectMode(CENTER)
    noLoop()

def draw():
    global rotsum
    background(235, 215, 182)
    for y in range(rows):
        rotsum += y*rotinc
        for x in range(cols):
            with pushMatrix():
                rotval = random(-rotsum, rotsum)
                translate(padding + (x*tilesize) - (0.5*tilesize) + (rotval*dampen),
                          padding + (y*tilesize) - (0.5*tilesize) + (rotval*dampen))
                rotate(radians(rotval))
                rect(0, 0, tilesize, tilesize)

Lediglich beim Schleifendurchlauf haderte ich mit Plaxcos Implementierung und an einigen der Parameter habe ich ein wenig herumgeschraubt, bis das fertige Bild meinen Vorstellungen entsprach. Und natürlich habe ich auch wieder meinen geliebten Packpapierhintergrund verwendet.

Was fängt man nun mit so einem Bild an?

Joachim Wedekind hatte Vorschläge mit gefüllten Quadraten und Kreisen, die dem Bild schon eine ganz andere Anmutung gaben:

cols = 12            # Anzahl der Spalten
rows = 22            # Anzahl der Reihen
tilesize = 32        # Kachelgröße
rotinc = 0.44        # Inkrementwert für die Rotation (in Grad)
rotsum = 0           # Rotation (in Grad)
padding = 3*tilesize # Abstand vom Fensterrand (rechts, links und oben, unten)
dampen = 0.45        # Dämpfungsfaktor

def setup():
    size((cols + 4)*tilesize, (rows + 4)*tilesize)
    this.surface.setTitle("Remixing Schotter: Bunte Quadrate")
    stroke(0)
    strokeWeight(2)
    rectMode(CENTER)
    noLoop()

def draw():
    global rotsum
    background(235, 215, 182)
    for y in range(rows):
        rotsum += y*rotinc
        fill(y*11, y*11, 255 - (y*22))
        for x in range(cols):
            with pushMatrix():
                rotval = random(-rotsum, rotsum)
                translate(padding + (x*tilesize) - (0.5*tilesize) + (rotval*dampen),
                          padding + (y*tilesize) - (0.5*tilesize) + (rotval*dampen))
                rotate(radians(rotval))
                rect(0, 0, tilesize, tilesize)

Die Version mit den Kreisen erhält man, wenn man die letzte Zeile des Sketches

                rect(0, 0, tilesize, tilesize)

durch

               circle(0, 0, tilesize)

ersetzt.

Eine weitere Möglichkeit wäre, die Quadrate, je tiefer sie nach unten fallen, auszublassen (Fade Out). Die finde ich vor allem darum interessant, weil dies mit der damaligen Plottertechnik nur sehr schwer bis gar nicht zu realisieren war. (An dem Processing.py-Sketch ändert sich eigenlich kaum etwas, ich habe ihn nur deswegen noch einmal vollständig abgedruckt, damit der Screenshot Platz auf der Seite findet.)

cols = 12            # Anzahl der Spalten
rows = 22            # Anzahl der Reihen
tilesize = 32        # Kachelgröße
rotinc = 0.44        # Inkrementwert für die Rotation (in Grad)
rotsum = 0           # Rotation (in Grad)
padding = 3*tilesize # Abstand vom Fensterrand (rechts, links und oben, unten)
dampen = 0.45        # Dämpfungsfaktor

def setup():
    size((cols + 4)*tilesize, (rows + 4)*tilesize)
    this.surface.setTitle("Remixing Schotter: Fade-Out")
    stroke(0)
    strokeWeight(2)
    rectMode(CENTER)
    noLoop()

def draw():
    global rotsum
    background(235, 215, 182)
    for y in range(rows):
        rotsum += y*rotinc
        # fill(y*11, y*11, 255 - (y*22), 255 - (y*11))
        fill(155, 0, 0, 255 - (y*11))
        for x in range(cols):
            with pushMatrix():
                rotval = random(-rotsum, rotsum)
                translate(padding + (x*tilesize) - (0.5*tilesize) + (rotval*dampen),
                          padding + (y*tilesize) - (0.5*tilesize) + (rotval*dampen))
                rotate(radians(rotval))
                rect(0, 0, tilesize, tilesize)

Ehrlich gesagt, weiß ich noch nicht, was ich hier eigentlich alles angestellt habe. Aber es hat einfach Spaß gemacht und daher hoffe ich, daß Ihr mit diesen und weiteren Ausflügen in die frühe Computerkunst ebenfalls Spaß haben werdet.

1 (Email-) Kommentar

Eine kleine Anmerkung zu deinem Posting über die Re-enactments kybernetischer Kunst: Algol ist wohl über die Entwicklerlinie eher mit Wirths späteren Sprachen verwandt, hat den Entwicklern von BASIC aber explizit als Grundlage für einige Konzepte in deren Sprachbau gedient. Hier zum Beispiel ein Zitat zur For-Next-Schleife:

The relation of BASIC to FORTRAN and ALGOL is apparent. From FORTRAN comes the order of the three loop-controlling values – initial, final, step– thus permitting the step size to be omitted if it is unity. From ALGOL comes the words "for" and "step", and the more natural testing for loop completion before executing the body of the loop. These and other similarities are not surprising, since we knew both languages, and we did not hesitate to borrow ideas.
Quelle: T. E. Kurtz (1978): BASIC. In: ACM SIGPLAN Notices, Vol. 13, No. 8, August 1978, pp- 103-118, hier: p. 107.

Kurtz erwähnt noch weitere Ähnlichkeiten und „Übernahmen” aus Algol in BASIC, betont aber an genauso vielen Stellen, dass sich Algol doch recht stark von BASIC unterscheidet und für didaktische Zwecke, wie sie Kurtz/Kemeny vorgeschwebt haben, nicht brauchbar war.
Ich habe in meinen Seminare zum Re-enactment Experimente gemacht, in denen wir versucht haben BBC-BASIC-Programme nach einer ähnlichen Struktur und ähnlichen Paradigmen zu programmieren, wie die Vorlagen der kyb. Künstler aus den 1960ern. Das hat (beispielsweise bei Georg Nees Programmen) gut funktioniert. Das benötigt allerdings modernere „Street BASIC”-Dialekte, die auch funktionales Programmieren erlauben.

– Stefan Höltgen (Kommentieren) (#)

(Kommentieren)