Mathematik mit TigerJython: Das Lotka-Volterra-System (2)

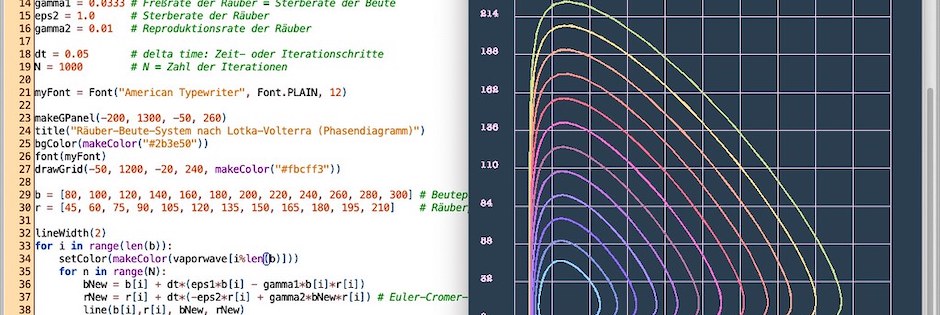
Ich kann momentan von TigerJython nicht lassen. Daher habe ich meine Experimente zur Lotka-Volterra-Gleichung mit der Erstellung eines Phasendiagramms für verschiedene Anfangspopulationen fortgesetzt. Denn ersetzt man die beiden Programmzeilen für den Plot in dem Programm von gestern mit der einen Zeile line(b, r, bNew, rNew), dann erhält man ein Phasendiagramm (die Dimensionen des Plotfensters müssen natürlich auch noch entsprechend angepaßt werden). Dabei werden auf der x-Achse die Anzahl der Beutetiere und auf der y-Achse die Anzahl der Räuber aufgetragen:

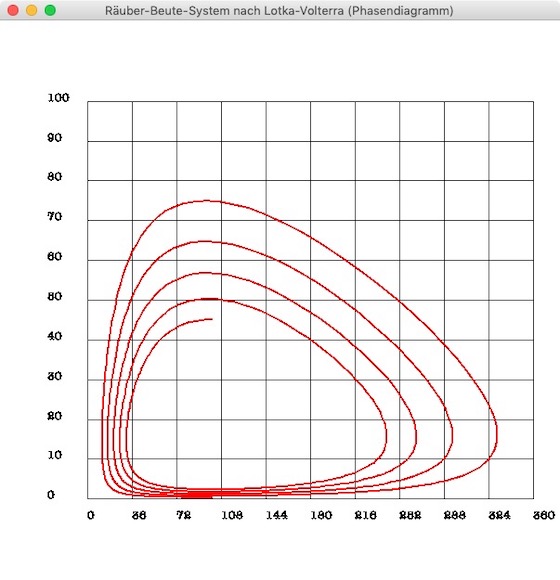
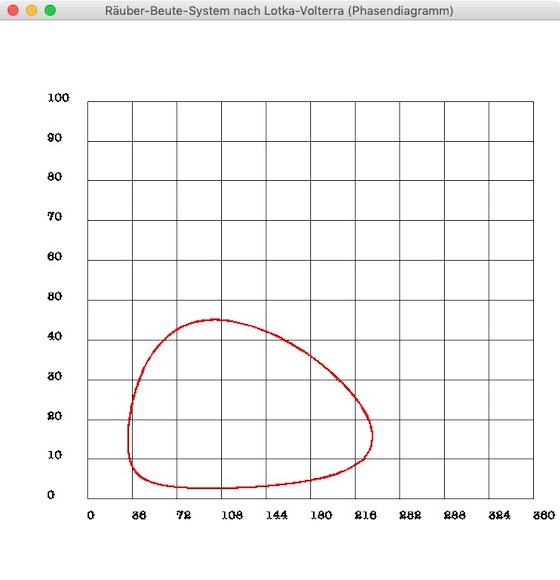
Der Screenshot oben zeigt das Phasendiagramm für die Lösung mit dem Eulerschen Polygonzuverfahren. Bei einem Phasendiagramm erkennt man deutlich, daß die (numerische) Lösung nicht periodisch ist und somit die zweite Lotka-Volterra-Regel verletzt. Löst man das System hingegen mit dem Euler-Cromer-Verfahren, bekommt man dieses Phasendiagramm:

Das ist eindeutig ein periodischer Verlauf, der immer wieder die gleichen Werte durchläuft. Nun ist es natürlich interessant, zu sehen, wie die Phasendiagramme bei unterschiedlichen Populationsstartwerten aussehen. Ich habe daher zwei Listen mit unterschiedlichen Startwerten erstellt:

b = [80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300] # Beutepopulationen
r = [45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210]    # Räuberpopulationen

Dann mußte natürlich das Programm zwei verschiedene Schleifen durchlaufen, erst einmal ein Hauptschleife, die über die beiden Listen iteriert und dann die darunterliegende Schleife, die – wie gehabt – die Zahl der jeweiligen Iterationen der Simulation durchläuft:

for i in range(len(b)):
    setColor(makeColor(vaporwave[i%len(b)]))
    for n in range(N):
        bNew = b[i] + dt*(eps1*b[i] - gamma1*b[i]*r[i])
        rNew = r[i] + dt*(-eps2*r[i] + gamma2*bNew*r[i]) # Euler-Cromer-Verfahren        
        line(b[i],r[i], bNew, rNew)
        b[i] = bNew
        r[i] = rNew

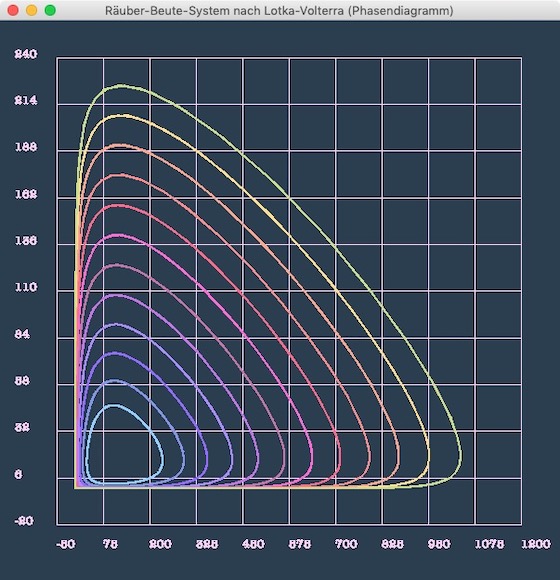
Da Mathematik ja schön ist und mensch das auch sehen soll, habe ich das Diagramm mit einer Farbpalette mit einer Vaporwave-ähnlichen Ästhetik aufgehübscht. Das Ergebnis kann sich tatsächlich sehen lassen:

Das komlette TigerJython-Skript für das Phasendiagramm sieht nun folgendermaßen aus:

# Lotka-Volterra-Gleichung mit dem Euler-Verfahren
# b = Beute
# r = Räuber

from gpanel import *

# Farbpalette
vaporwave    = ["#94d0ff", "#8795e8", "#966bff", "#ad8cff",
                "#c774e8", "#c774a9", "#ff6ad5", "#ff6a8b",
                "#ff8b8b", "#ffa58b", "#ffde8b", "#cdde8b",
                "#8bde8b", "#20de8b"]

eps1 = 0.5      # Reproduktionsrate der Beute
gamma1 = 0.0333 # Freßrate der Räuber = Sterberate der Beute
eps2 = 1.0      # Sterberate der Räuber
gamma2 = 0.01   # Reproduktionsrate der Räuber

dt = 0.05       # delta time: Zeit- oder Iterationschritte
N = 1000        # N = Zahl der Iterationen

myFont = Font("American Typewriter", Font.PLAIN, 12)

makeGPanel(-200, 1300, -50, 260)
title("Räuber-Beute-System nach Lotka-Volterra (Phasendiagramm)")
bgColor(makeColor("#2b3e50"))
font(myFont)
drawGrid(-50, 1200, -20, 240, makeColor("#fbcff3"))

b = [80, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300] # Beutepopulationen
r = [45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210]    # Räuberpopulationen

lineWidth(2)
for i in range(len(b)):
    setColor(makeColor(vaporwave[i%len(b)]))
    for n in range(N):
        bNew = b[i] + dt*(eps1*b[i] - gamma1*b[i]*r[i])
        rNew = r[i] + dt*(-eps2*r[i] + gamma2*bNew*r[i]) # Euler-Cromer-Verfahren        
        line(b[i],r[i], bNew, rNew)
        b[i] = bNew
        r[i] = rNew
print("I did it, Babe!")

Man kann das Lotka-Volterra-System natürlich noch weiter aufbohren. Zum Beispiel könnte man für die Beutepopulation begrenzte Ressourcen vorsehen oder sich fragen, was passiert, wenn zwei verschiedene Räuberarten sich um die Beute streiten. Vielleicht stelle ich das eine oder andere hier auch noch vor. Still digging!

(Kommentieren)