Tutorial: Einen Pythagoras-Baum mit der NodeBox zeichnen

Gestern abend konnte ich es nicht lassen. Ich war zu neugierig, ich mußte unbedingt noch mit der neuen Version von Karsten Wolfs NodeBox-Fork spielen. Insbesondere interessierte mich, wie groß die Unterschiede zwischen Processing.py, dem Python-Mode von Processing und der NodeBox sind, da NodeBox 1 sich ja explizit auf Processing als Inspiration beruft.

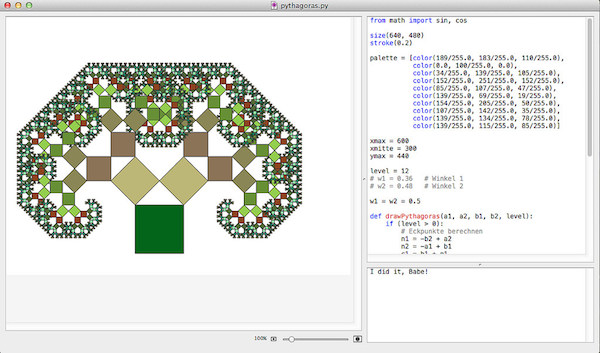
Also habe ich mir als (schnell durchzuführendes) Projekt die Programmierung eines Pythagoras-Baumes ausgedacht, da ich diesen ja schon einmal in Processing.py programmiert hatte. Und wenn man sich den Nodebox-Quellcode unten anschaut und ihn mit dem Processing.py-Quellcode vergleicht, stellt man fest: Die Unterschiede sind minimal.

from math import sin, cos

size(640, 480)
stroke(0.2)

palette = [color(189/255.0, 183/255.0, 110/255.0),
           color(0.0, 100/255.0, 0.0),
           color(34/255.0, 139/255.0, 105/255.0),
           color(152/255.0, 251/255.0, 152/255.0),
           color(85/255.0, 107/255.0, 47/255.0),
           color(139/255.0, 69/255.0, 19/255.0),
           color(154/255.0, 205/255.0, 50/255.0),
           color(107/255.0, 142/255.0, 35/255.0),
           color(139/255.0, 134/255.0, 78/255.0),
           color(139/255.0, 115/255.0, 85/255.0)]

xmax = 600
xmitte = 300
ymax = 440

level = 12
w1 = 0.36   # Winkel 1
w2 = 0.48   # Winkel 2

# w1 = w2 = 0.5

def drawPythagoras(a1, a2, b1, b2, level):
    if (level > 0):
        # Eckpunkte berechnen
        n1 = -b2 + a2
        n2 = -a1 + b1
        c1 = b1 + n1
        c2 = b2 + n2
        d1 = a1 + n1
        d2 = a2 + n2
        # Start-Rechteck zeichnen
        fill(palette[(level-1)%10])
        beginpath(a1 + xmitte, ymax - a2)
        lineto(b1 + xmitte, ymax - b2)
        lineto(c1 + xmitte, ymax - c2)
        lineto(d1 + xmitte, ymax - d2)
        endpath()
        e1 = d1 + w1*(c1 - d1) + w2*n1
        e2 = d2 + w1*(c2 - d2) + w2*n2
        # Schenkel-Quadrate zeichnen
        drawPythagoras(e1, e2, c1, c2, level-1)
        drawPythagoras(d1, d2, e1, e2, level-1)

drawPythagoras(-(xmax/10), 0, xmax/20, 0, level)

print("I did it, Babe!")

Die Tropfenschachtel kennt den schönen width-Befehl nicht (den übrigens der leider nicht mehr gepflegte NodeBox-Nachfolger PlotDevice kannte), daher muß der eigentliche Zeichenvorgang stattdessen mit beginpath() und endpath() geklammert werden. Und statt vertex() sind die Befehle moveto() und lineto() zu verwenden ¹.

Ansonsten mußte ich noch alle Farbwerte in der Liste zu Beginn des Programms durch 255.0 ² teilen, da die Nodebox RGB-Werte (float) zwischen 0.0 und 1.0 erwartet und keine int zwischen 0 und 255 wie Processing. Ansonsten laufen ja beide Umgebungen mit Python 2.7 und so waren keine weiteren Überraschungen festzumachen.

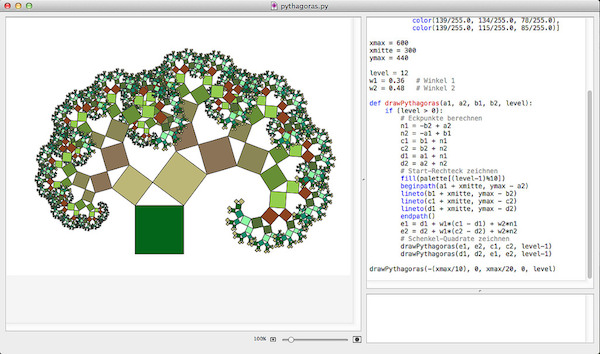
Ersetzt man übrigens die beiden Winkelwerte in den Zeilen

w1 = 0.36   # Winkel 1
w2 = 0.48   # Winkel 2

durch die (im obigen Quelltext auskommentierte) Zeile

w1 = w2 = 0.5

so erhält man einen symmetrischen Pythagoras-Baum. Und natürlich lädt so eine einfach zu bedienende Entwicklungsumgebung wie die NodeBox schnell zu weiteren Spielereien ein. Das hat sie mit Processing gemein. Der Sprung von Java zu Python (nicht Jython!) ist ihr also durchaus gelungen. Und mit der Integration von Numpy, SciPy und den anderen Paketen sind natürlich noch viele andere Dinge möglich, die mit Processing nicht (so einfach) gehen ³. Still digging!

---

1 (Email-) Kommentar

---

Die Byte basierten "color()" Befehle kann man in NodeBox einfach mit einem vorangestellten "colormode(range=255.0)" erzeugen. Siehe https://www.nodebox.net/code/index.php/Reference_|_colormode()
colormode(range=255.0)
palette = [color(189, 183, 110), color(0.0, 100, 0.0), color(34, 139, 105), color(152, 251, 152), color(85, 107, 47), color(139, 69, 19), color(154, 205, 50), color(107, 142, 35), color(139, 134, 78), color(139, 115, 85)]

– Karsten Wolf (Kommentieren) (#)

---

(Kommentieren)