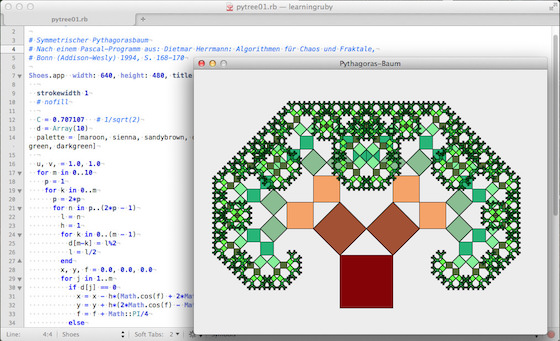
Shoes, Shapes, Schildkröten und der Baum des Pythagoras

Mit dem Slot shape(left, top) {…} kann man in Shoes, dem kleinen, plattformübergreifenden GUI- und Graphik-Toolkit für Ruby einen Block festlegen, in dem man dann so etwas wie eine Variante der Turtle-Graphik realisieren kann. Die Befehle, die innerhalb dieses Blocks interpretiert werden können, sind move_to, line_to und arc_to. Ich habe die ersten beiden Kommandos mal genutzt, um mit Shoes einen symmetrischen Pythagorasbaum zu zeichnen.

Da die Konstruktion dieses Fraktals sich zwar recht einfach aus dem Satz des Pythagoras erklärt, die Formulierung im Programm aber nicht trivial ist, habe ich den Algorithmus dem Buch »Algorithmen für Chaos und Fraktale« von Dietmar Hermann aus dem Jahre 1994 entnommen, das wohl mittlerweile so selten ist, daß Amazon für ein gebrauchtes Exemplar einen horrenden Preis verlangt. Und ich habe darauf verzichtet, den Algorithmus rekursiv zu formulieren, obwohl man das durchaus kann. Denn die gewählte Iterationstiefe ist zehn (0…10) und ob Shoes das als Rekursion vertragen hätte, da bin ich nach meinen letzten Erfahrungen doch sehr skeptisch. Aber jede Rekursion läßt sich in eine Iteration umformulieren und vice versa.

Um das Resultat ein wenig aufzuhübschen, habe ich mit

palette = [maroon, sienna, sandybrown, darkseagreen, mediumseagreen, lightgreen,
           darkolivegreen, lawngreen, forestgreen, green, darkgreen]

ein Palette mit einigen aus den in Shoes vordefinierten Farben erzeugt, die in etwa von dunkelbraun über hellere Brauntöne zu leichten Grüntönen bis hin zu einem Dunkelgrün übergehen sollten. Denn der symmetrische Pythagorasbaum sieht noch nicht wirklich wie ein Baum aus und da sollten die Farben wenigstens eine gewisse Illusion erzeugen.

Und hier der komplette Quellcode zum Nachprogrammieren:

# encoding: utf-8

# Symmetrischer Pythagorasbaum
# Nach einem Pascal-Programm aus: Dietmar Herrmann: Algorithmen für Chaos und Fraktale,
# Bonn (Addison-Wesly) 1994, S. 168-170

Shoes.app  width: 640, height: 480, title: "Pythagoras-Baum", resizable: false do
  
  strokewidth 1
  background white
  
  C = 0.707107   # 1/sqrt(2)
  d = Array(10)
  palette = [maroon, sienna, sandybrown, darkseagreen, mediumseagreen, lightgreen,
             darkolivegreen, lawngreen, forestgreen, green, darkgreen]
  
  u, v, = 1.0, 1.0
  for m in 0..10
    p = 1
    for k in 0..m
      p = 2*p
      for n in p..(2*p - 1)
        l = n
        h = 1
        for k in 0..(m - 1)
          d[m-k] = l%2
          l = l/2
        end
        x, y, f = 0.0, 0.0, 0.0
        for j in 1..m
          if d[j] == 0
            x = x - h*(Math.cos(f) + 2*Math.sin(f))
            y = y + h*(2*Math.cos(f) - Math.sin(f))
            f = f + Math::PI/4
          else
            x = x + h*(Math.cos(f) - 2*Math.sin(f))
            y = y + h*(2*Math.cos(f) + Math.sin(f))
            f = f - Math::PI/4
          end
          h = C*h
        end
        u = h*(Math.cos(f) + Math.sin(f))
        v = h*(Math.cos(f) - Math.sin(f))
        shape do
          fill palette[m]
          move_to((48*(x - v + 6.5)).round, 480-(48*(y - u + 2)).round)
          line_to((48*(x + u + 6.5)).round, 480-(48*(y - v + 2)).round)
          line_to((48*(x + v + 6.5)).round, 480-(48*(y + u + 2)).round)
          line_to((48*(x - u + 6.5)).round, 480-(48*(y + v + 2)).round)
          line_to((48*(x - v + 6.5)).round, 480-(48*(y - u + 2)).round)
        end
      end
    end
  end
end

Noch mehr Schuhe im Schockwellenreiter

• Keiner kennt Shoes
• Keiner kennt Shoes (2): Bilder und Links
• Keiner kennt Shoes (3): Das Demokratie-Spiel
• Brandneue Schuhe, denn keiner kennt Shoes
• Keiner kennt Shoes (4): Spieleprogrammierung
• Keiner kennt Shoes: GUI 95 (1)
• Keiner kennt Shoes: GUI 95 (2)
• Keiner kennt Shoes: Widgets (1)
• Keiner kennt Shoes: Widgets (2)
• Ein (weiteres) Abenteuer mit Shoes
• Running Orcs mit Shoes
• Spaß mit Shoes: Action!
• Shoes und SVG in einer Zeile
• Animationen Shoes Style
• Spaß mit Shoes 3.3.1: Video
• Noch mehr Spaß mit dem Shoes Video-Widget
• Shoes zieht Kreise
• Und Action! Noch mehr Spaß mit Shoes
• Neue Shoes Beta mit Plot Widget
• Cantors Doppelkäse mit Shoes

(Kommentieren)